issue contents
March 2014 issue
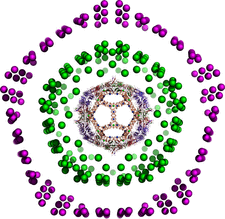
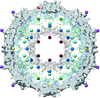
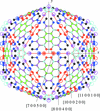
Cover illustration: Viruses and fullerenes obey similar mathematical constraints. Point arrays derived from affine symmetries provide blueprints both for the organization of material in a virus (here Pariacoto virus, middle) and for the atomic positions in nested fullerene cages called carbon onions (here the carbon onion C60-C240-C540, C60 not shown), showing that affine symmetry is a common thread in biology and chemistry [Dechant et al. (2014). Acta Cryst. A70, 162-167].
mathematical crystallography
research papers
foundations
research papers
book reviews



 journal menu
journal menu