Group-theoretical methods are used to enumerate the structures of ordered perovskites, in which 1:2 and 1:3 ordering of B and B′ cations is considered in combination with the ubiquitous BX6 (or B′X6) octahedral tilting. The cation ordering on the B-cation site is described by irreducible representations of the 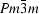 space group of the cubic aristotype: Λ1 (k = 1/3,1/3,1/3) for the cation ordering pattern in the 1:2 compound A3BB
space group of the cubic aristotype: Λ1 (k = 1/3,1/3,1/3) for the cation ordering pattern in the 1:2 compound A3BB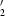 X9 and
X9 and 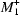 (k = 1/2,1/2,0) for the cation ordering in the 1:3 compound A4BB
(k = 1/2,1/2,0) for the cation ordering in the 1:3 compound A4BB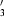 X12. The octahedral tilting is mediated by the irreducible representations
X12. The octahedral tilting is mediated by the irreducible representations 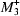 and
and 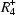 . Ten distinct structures have been identified in the 1:2 case and 11 structures for 1:3.
. Ten distinct structures have been identified in the 1:2 case and 11 structures for 1:3.

 journal menu
journal menu











