The puzzle-interlayer model: an approach to the analysis of tightly packed arrangements of hard particles

Gille, W.

doi:10.1107/S0021889806055130

conference papers

JOURNAL OF
APPLIED
CRYSTALLOGRAPHY

ISSN: 1600-5767

Volume 40| Part s1| April 2007| Pages s691-s695

doi:10.1107/S0021889806055130

The puzzle-interlayer model: an approach to the analysis of tightly packed arrangements of hard particles

Wilfried Gille ^a ^*

^aMartin-Luther-University Halle-Wittenberg, SAS-Laboratory, Hoher Weg 8, D-06120 Halle, Germany
^*Correspondence e-mail: [email protected]

(Received 14 August 2006; accepted 19 December 2006; online 20 January 2007)

The small-angle scattering (SAS) structure functions are analyzed for an idealized, random two-phase system: a stationary arrangement of hard puzzle particles, separated by a relatively thin interspace, which can be approximated by an interlayer. The detailed shape of the interlayer is defined by the shape of the particles themselves: The starting point for producing these initial particles is a three-dimensional initial puzzle $[{P_0}]$ in the state of tessellation. Its pieces, homogeneous particles of random shape, fit together filling the space. In a second step, an expanded puzzle $[{P_{\tau }}]$ is constructed by translating the initial particles by a certain length $[\tau]$ (relative to one another). The whole tightly packed particle arrangement depends on $[{P_0}]$ . The interlayer region between the particles is a connected, homogeneous region. The SAS intensity of $[{P_{\tau }}]$ depends on the parameter $[\tau]$ and on the typical shape and size of the pieces of $[{P_0}]$ . Chord length distributions (CLDs) are used in the description. The random shape of the pieces of $[{P_0}]$ possesses a CLD 1. The CLD 2 of the intermediate spaces is approximated by that of an idealized layer of constant thickness $[\tau]$ . The scattering of $[{P_{\tau}}]$ results in terms of the CLDs of both phases. The approach can be applied to many types of $[{P_0}]$ . Two initial tessellations of $[{P_0}]$ are studied, a `dead leaves' tessellation produced by spherical primary grains and the Poisson plane mosaic.

Keywords: small-angle scattering; structure functions; tessellation; particle packing arrangements.

1. Introduction

There are several approaches in the field of small-angle scattering (SAS) for random two-phase systems, where the particle shape or the particle arrangement, or both, are defined by a stochastic model (Porod, 1952a ,b ; Debye et al., 1957 ; Chen et al., 1991 ; Levitz & Tchoubar, 1992 , and others). A survey was given by Hermann (1991 ) and by Torquato (2002 ). In this paper, a new approach named puzzle-interlayer model (PIM) is added to those methods. This approach is based on the construction of arrangements of hard particles as illustrated in Fig. 1. A tessellation is given. It involves random pieces (the subsequent particles), the separation of which followed by a certain translation constitutes the PIM. The two-dimensional puzzle (Fig. 1) can be extended to three dimensions (two- or three-dimensional scatterer). The fact that the tightly packed particles on the right-hand side of Fig. 1 were regions of a random tessellation before leads to the following conclusions: It will be possible to determine SAS structure functions, including the scattering intensity I(h) [ $[h = 4\pi \sin(\theta)/\lambda]$ , $[2\theta]$ = scattering angle, $[\lambda]$ = wavelength of radiation], in terms of inherent properties of the initial tessellation. Its origin can be manifold. Any starting mosaic, the real structure functions of which are well investigated, can be operated with. Then, the only parameter of the approach is a length parameter, describing the shifting of the pieces. The analysis of the information involved in a section (see also Fig. 2) is the subject of stereology, but is not part of the calculations here. Based on the theory of chord length distributions (CLDs), two PIMs will be considered: First, a spatial tessellation can be constructed from a general `dead leaves' model (DLM) (Serra, 1982 , pp. 508–509). Based on the analytic expressions describing the DLM tessellation type (see Gille, 2003 ), a PIM with DLM puzzle pieces is studied (§3.1). Second, the Poisson plane tessellation (Hermann, 1991, pp. 13–15) can also be used as the originating mosaic of a PIM (§3.2).

Figure 1
Tessellation $[{P_0}]$ and puzzle $[{P_{\tau}}]$ . Although infinite tessellations are discussed, an illustrative representation requires a finite planar- or spatial section. Thus, the border pieces of the tessellation additionally reflect the shape of the quadratic section.

Figure 2
A plane PIM and the CLDs $[\varphi]$ and f. (a) All PPs of the initial puzzle $[{P_0}]$ exactly fit together, no intermediate space, $[\tau \equiv 0]$ . (b) Modification of $[{P_0}]$ by a shifting process produces small intermediate layers $[\tau]$ , $[\tau \rightarrow 0]$ . (c) A magnified section of (b).

2. Properties of the model

In the initial tessellation $[{P_0}]$ , gaps between one and the next puzzle piece (PP) do not exist. By `expanding' $[{P_0}]$ an expanded puzzle $[{P_{\tau}}]$ results. The random shape of the PPs is defined by $[{P_0}]$ . Key parameters of $[{P_{\tau}}]$ are the volume fraction c of the PPs and the shifting-length parameter $[\tau]$ .

2.1. The initial puzzle $[{\bi P}_{\bf 0}]$

The largest PP has the largest diameter L₀, e.g. $[{L_0}\simeq 2]$ –20 nm. The sample size is several orders of magnitude greater than L₀. The assembly of randomly shaped PPs allows a complete filling of the space, later fulfilling the condition for an isotropic scatterer. Let the (electron) density inside all the PPs be constant. For $[{P_0}]$ the lines (interfaces) of separation between the PPs are infinitely thin. The whole sample volume consists of the PP phase, phase 1. Thus, for $[{P_0}]$ no SAS effect can be expected. In the following, all the PPs change neither shape nor size or inner constitution (no change of the homogeneity inside the PPs). The characteristic shape and size of the pieces of $[{P_0}]$ are the first component for determining I(h) of the particle arrangement $[{P_{\tau}}]$ .

2.2. The expanded puzzle $[ \bi P_{\tau}]$

A slightly modified (but not mixed or even distorted) puzzle $[P_{\tau}]$ results, after translating all the PPs one by one, approximately by a length $[\tau]$ , $[0 \,\lt\, \tau \,\lt\, {L_0}]$ (Fig. 1). The length $[\tau]$ can be detected perpendicularly to the touching PP surfaces. Simply said, $[\tau]$ is the typical distance between two neighboring PP interfaces (see Figs. 1, 2 and 3). Let the PPs be embedded in a second phase of constant (electron) density (Fig. 2b). Particle arrangements $[{P_{\tau}}]$ involving intermediate layers result. It is simple `to move back' $[{P_{\tau}}]$ to $[{P_0}]$ , without any rotation or exchange of any two PPs. The larger $[\tau]$ , the greater the volume fraction c of the connected interlayer phase 2.

Figure 3
A cubic section of a mosaic P₀ of a model sample involving PPs resulting from Poisson polyhedra. Specific translations $[\tau]$ lead to specific $[P_{\tau}]$ .

If $[\tau]$ is not too small and if the (electron) density in the newly produced connected intermediate regions differs from that of the PPs, $[{P_{\tau}}]$ will lead to a clear isotropic SAS. The large number N of PPs allows fulfillment of the condition of an isotropic scatterer. The random shapes of the PPs cannot be arbitrary, as they must be able to completely fit together without intermediate spaces, $[c\rightarrow 1]$ for $[\tau \rightarrow 0]$ . On the one hand, this requirement is not fulfilled by spherical, hemispherical or conical PPs, which cannot act as PPs in the PIM. On the other hand, cubes or parallelepipeds with matching edge lengths cannot be inserted as PPs either. Such trivial `stone by stone samples' do not fulfill the requirement of isotropy.

2.3. The chord length distributions of $[\bi P_{\tau}]$

The analysis of I(h) of $[{P_{\tau}}]$ is hard to achieve based on elementary methods (Feigin & Svergun, 1987 ). In the present approach, CLDs are operated with. Whatever the origin of a random two-phase system, two CLDs $[\varphi (l)]$ and f(m), simultaneously considered, define the SAS correlation function (CF) $[\gamma (r)]$ and I(h) (Méring & Tchoubar, 1968 ; Levitz & Tchoubar, 1992). Details, concerning the kernels of the integral transformations, connected with the functions $[\gamma(r)]$ and $[\gamma^{\prime \prime}(r)]$ are analyzed by Burger & Ruland (2001 ). A theoretical example was analyzed (Gille, 2005 ). Let $[\varphi (l)]$ be the CLD of the PP phase (isotropic uniform random chord lengths l_i in phase 1) and f(m) that of the intermediate spaces (chord lengths m_i in the connected phase 2) (Fig. 2c). The system $[{P_0}]$ involves the property $[f(m) = \delta (m)]$ . The mean chord length $[\overline{m}]$ disappears, $[\overline{m} \equiv 0]$ . On the other hand, $[{P_{\tau}}]$ has a limiting property: If $[\tau \rightarrow \infty]$ then $[\overline{m} \rightarrow \infty]$ and $[f(m)\rightarrow 0]$ results. The function $[\varphi (l)]$ and its first moment $[\overline {l} = 4{V_0}/{S_0}]$ describe the PPs with average volume V₀ and average surface area S₀. This was discussed for non-convex particles (Mazzolo et al., 2005 ). The shape of phase 2 is defined by the shapes of the PPs.

2.4. Chord length distribution densities, specific functions and I(h)

For independent segment lengths l_i and m_i, there are comprehensive equations (see Cox, 1963 ; Weil, 2004 ; Gille, 2002 ). Equations (1)–(3) connect the functions $[\varphi (l)]$ and f(m) with the SAS CF $[\gamma (r)]$ and I(h). The CLDs define the corresponding characteristic functions p(t) and q(t),

$[p(t) = \textstyle\int\limits _{0}^{\infty }{\exp(i t r)}\, \varphi (r) \, {\rm d} r, \quad q(t) = \int\limits _{0}^{\infty }{\exp(i t r)}\, f(r) \, {\rm d} r. \eqno (1)]$

A working function Q(t) is defined in terms of the CF via $[g(r) = \gamma ^{\prime \prime}(r)/|\gamma ^{\prime}(0)|+2\delta(r)]$ ,

$[Q(t) = \textstyle\int\limits _{0}^{\infty }{\exp(i t r)}\, g(r) \,{\rm d} r. \eqno (2)]$

Furthermore, the function Q(t), involving a real part and an imaginary part, is related to p(t) and q(t):

$[Q(t) = {{p(t)+q(t)-2 p(t)\, q(t)}\over{1-p(t)\, q(t)}}. \eqno (3)]$

At the origin, $[\Im [Q(0)] = 0]$ and Q(0) = 1 follows. Equation (3) allows the determination of Q(t) if both $[\varphi]$ and f are known (Méring & Tchoubar, 1968). By combining equation (3) with the inverse transformation of equation (2), the function g(r) of the particle arrangement,

$[\eqalignno{g(r) =\ &{{1}\over{2 \pi}} \int\limits _{-\infty }^{\infty}{\exp(-i t r)} \, Q(t) \, {\rm d} t \cr =\ &{{1}\over{\pi}} \int\limits _{0}^{\infty} \left\{ \cos (t r) \, \Re [Q(t)] + \sin (t r) \, \Im[Q(t)] \right\} \,{\rm d} t, &(4)}]$

is obtained (Gille, 2005). For all r, $[\Im[g(r)]\equiv 0]$ . The normalized scattering intensity, I(0) = 1, basically results from $[I(h) = 4\pi/{v_{\rm c}}\int_{0}^{\infty} r^2 \gamma(r)\sin(h r)/(h r)\, {\rm d}r]$ . More tailormade for the actual case, I follows in terms of g (Gille, 2005, Appendix B, p. 526),

$[I(h) = {{4 \pi}\over{v_{\rm c} \, l_{\rm p}}} \int\limits _{0}^{\infty}g(r)\, {{2-2 \cos(h r)-h r \sin(h r)}\over{{h^4}}}\, {\rm d} r. \eqno (5)]$

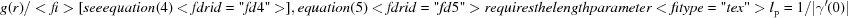Besides [g(r)/<fi> [see equation (4)<fdr id= ], equation (5) requires the length parameter {l_{\rm p}} = 1/|\gamma ^{\prime} (0)|]" class="img_align_bottom" style="max-width: 100%; height: auto; width: 848px;" /> and the characteristic volume v_c (Porod, 1952a). These parameters can be traced back to Q(t) [see equations (11) and (12), Appendix A]. Summing up both integral transformations, equations (4) and (5), enables the determination of I(h) in terms of Q(t) via one transformation step.

2.5. I(h) in terms of Q(t)

Assuming a certain order range L in the system, equation (5) connects g(r) with I(h). Inserting equation (4) into equation (5) gives

$[I(h) = {{2}\over{{v_{\rm c}}\, {l_{\rm p}}}}\int\limits _{-\infty }^{\infty }T(h,L,t)\, Q(t) \,{\rm d} t. \eqno (6)]$

Thus, I(h) can be traced back to Q(t) and to a function T(h,L,t), defined in Appendix B [see equations (16)–(19)]. The working function Q(t) depends on the actual CLDs for $[0 \,\lt\, r \,\lt\, L]$ . For a selected L of the system, Q(t) is fixed in terms of $[\varphi]$ and f via equations (1)–(3). Now, Q(t), g(r) and I(h) will be derived for two cases.

3. Analysis of three-dimensional puzzle-interlayer models

Each initial system $[{P_0}]$ defines a specific PIM. However, there is a natural restriction: The calculation steps, described for any special PP type, require that the CLD $[\varphi (l)]$ of the selected tessellation type has already been investigated. This is the case with the DLM puzzle (Gille, 2003), as well as with PPs belonging to the so-called Poisson tessellation (Stoyan et al., 1995 ; Hermann, 1991).

The two cases (see Figs. 2 and 3) possess a common property, which results from the assumption $[\tau \,\lt\, {L_0}]$ , say $[4 \tau \leq {L_0}]$ : The CLD f(m) of the interlayer region can be approximated by that of a single layer (lamella). The smaller the ratio $[\tau /{L_0}]$ , the better f(m) can be approximated by $[f(m) = 2{{\tau }^2}\big/{m^3}]$ ( $[\tau \,\lt\, m \,\lt\, \infty]$ ). The first moment $[\overline{m}]$ obeys $[\overline{m} = 2\tau]$ . Higher moments do not exist. According to equation (1), q(t) can be represented in terms of the incomplete $[\Gamma]$ function

$[q(t,\tau) = {\exp( i t \tau )} \,(1+i t \tau)-{t^2} {{\tau }^2} \Gamma (0,-i t \tau). \eqno (7)]$

Equation (7) is used to determine the SAS structure functions of two special PIMs.

3.1. A `dead leaves' puzzle-interlayer model

For PPs defined by a DLM, a complete set of formulas describing the PPs is known (Serra, 1982). Based on spherical grains of diameter d, a DLM puzzle can be constructed (Gille, 2003) (see Fig. 2). The CLD $[\varphi (l,d)]$ of the PPs is

$[\varphi (r,d) = {{2}\over{9 d}} \left [1+100 \left({{d}\over{2d+3r}}\right)^3 \right] . \eqno (8)]$

The function q(t) [equation (1)] can be represented by two terms involving the exponential integral function. The CLD possesses the property $[\varphi (0,d) = 3/d]$ . The PPs are described by the first moment $[\overline{l} = d/3]$ and by a radius of gyration $[{R_{\rm G}}\simeq 0.372d]$ . Equations (1)–(4) give Q(t) and g(r). For selected relative length parameters, d = 2 and $[\tau]$ = 0.5, the functions g(r) (Fig. 4) as well as I(h) and the Porod plot P₁(h) (Fig. 5) result by numerical integration.

Figure 4
CLDs of a PIM based on a DLM tessellation with relative length parameters $[d, \tau]$ . The pure CLDs are shown in the insert. The behavior of the function g(r) significantly reflects the relative length parameters d = 2 and $[\tau = 0.5]$ .

Figure 5
Normalized scattering intensity $[I(h , \overline l)]$ and Porod plot $[P_1(h , 2\tau)]$ for a DLM-PIM. The full line describes the scattering of a single lamella of thickness $[\tau]$ .

The function g(r) possesses a singularity (finite jump) at $[r = \tau]$ , originating from the CLD of the lamella (Fig. 4 insert). For $[r \,\lt\, \tau]$ , the function $[\varphi (l)]$ defines the behavior of g(r). For the PIM considered, $[g(0) = \varphi(0)]$ is obtained. In the actual case of smooth primary grains, the parameter $[\overline{l}]$ results from $[\overline{l} = 1/\varphi(0) = 1/g(0)]$ . For larger r, $[\tau \,\lt\, r \,\lt\, L]$ , the CLDs $[\varphi]$ and f are intermixed and both define the behavior of g(r), according to equations (2) and (3). In two r intervals, $[g \,\lt\, 0]$ . The first local minimum is connected with both parameters, d and $[\tau]$ . It cannot be interpreted as a distinctive length of the model.

The PIM parameters can be obtained from scattering intensities (Fig. 5). For relatively large h values, a normalized Porod plot, $[{P_1}(h) = {v_{\rm c}}{l_{\rm p}} \,I(h,d,\tau)\, {h^4}/(8\pi)]$ , reflects the scattering of a single lamella, $[{P_1}(h,\tau) = 2\tau \,{v_c}{l_p} \,{{\sin(2\tau h/4)}^2}/(2\pi)]$ . The model parameter d, intermixed with this asymptotic behavior, can be detected observing $[I(h,\overline l,\tau)]$ at relatively small h, e.g. $[h \,\lt\, 10/d]$ . The shoulder at h = h_s (Fig. 5, left-hand side plot) reflects the PP size via $[h_{\rm s} \, \overline l = 2\pi]$ . Evidently, the determination of the parameter $[\tau]$ is simpler than that of $[\overline l]$ , d, as the PPs do not have a fixed shape.

3.2. The puzzle-interlayer model based on Poisson polyhedra

In the Poisson polyhedra case, the boundaries of the PPs inside the cubic section (Fig. 3) are planes. Such a tessellation is generated by planes, homogeneously and isotropically distributed in space. This model has been thoroughly investigated in stochastic geometry (Stoyan et al., 1995 ; Weil, 2004). It is frequently used in materials science (Hermann, 1991) and involves one free parameter. The randomly shaped PPs are described by $[\varphi(l)]$ , reflecting geometric properties of the tessellation. Let $[\overline{l}]$ be the first moment. Then $[\varphi (l) = (1/\overline{l})\exp \big(-l/\overline{l}\big)]$ . The radius of gyration R_G of the PPs is $[{R_{\rm G}} = 2(3)^{1/2}\overline{l}]$ .

The expression $[p(t) = i /(i +\overline{l} t)]$ results from equation (1). Applying equations (3) and (4) for selected parameters $[\overline{l}]$ and $[\tau]$ , g(r) follows. Inserting the corresponding relative length parameters (here $[\overline{l} = 1]$ instead of d), Fig. 6 results. The first moment of $[\varphi (l)]$ is indicated by g(0+) via $[\overline{l} = 1/g(0+)]$ . The position of the finite jump indicates $[\tau]$ . These parameters reflect the intrinsic properties of the CLDs (see the insert of Fig. 6). Two different representations of the scattering intensity functions enable the detection of the model parameters. Analogously, $[\overline{l}]$ is connected with a shoulder in I, and P₁ is qualified for detecting $[\tau]$ (Fig. 7).

Figure 6
Real structure functions of a PIM based on the Poisson mosaic. The function g(r) reflects the relative length parameters $[\overline{l} = 1]$ and $[\tau = 0.5]$ . A graph of the CLDs $[\varphi]$ and f is shown in the insert.

Figure 7
The functions $[I(h \, \overline l)]$ and Porod plot $[{P_1}(h\, 2 \tau)]$ for a Poisson polyhedra PIM (see Figs. 3 and 6). The full line describes the asymptotic approximation.

4. Summary and conclusions

The approach describes isotropic arrangements of tightly packed homogeneous particles, a two-phase system of non-overlapping particles of random but fixed shapes. For this purpose, CLDs are applied. Shape specification is inherent in the PIM, so pair correlation functions need not be operated with. The shape of the PPs is random, but not arbitrary.

Parameters that result from an infinitely diluted arrangement of PPs [CF, CLD, R_G, I₀(h), P₁(h), l_c, f_c, v_c], describe a single PP (Gille, 2003). The volume fraction c of the PIM approach is defined by the particle size of the PPs (parameters d, $[\overline{l}]$ ) and by the interlayer thickness $[\tau]$ (parameter $[\overline{m} = 2 \tau]$ ) by the equation $[c = \overline{l}/\big(\overline{l}+2\tau \big)]$ . The fact that the PPs of a three-dimensional initial puzzle $[{P_0}]$ fit together and occupy the space completely is reflected by $[\varphi (0) = 1/\overline{l}]$ . This equation is connected with the construction of the PPs. So, the attempt to use spherical PPs of diameter D, characterized by $[\varphi (l) = 2l/{D^2}]$ ( $[0\leq l \,\lt\, D]$ ), results in $[\varphi (0) = 0\neq 1/ \overline {l}]$ . Thus, there is a discrepancy between the positive length $[\overline{l} = 2D/3]$ and $[\varphi (0)]$ . An attempt to form a puzzle from arbitrary smooth single particles will result in contradictions. For the large class of PPs constructed from a DLM tessellation originating from smooth grains [second derivative of the grain CF $[{{\gamma }_{\rm G}}^{\prime \prime}(0) = 0]$ ], $[\varphi (0) = 1/\overline{l}]$ is a characteristic property. The Poisson mosaic case is not so far from an elementary DLM. In both cases, the analysis of the CFs $[{{\gamma}_{\rm P}}(r)]$ of the PPs leads to $[{{\gamma }_{\rm P}}^{\prime \prime}(0) = 1/{{(\overline{l})}^2}]$ . Additionally, $[{{\gamma }_{\rm P}}(r) = \exp(-r/\overline{l})]$ in the Poisson mosaic case. In the most general DLM case (Serra, 1982), the function $[\varphi]$ is connected with the particle CF $[{{\gamma }_{\rm P}}]$ via $[\varphi (0+) = [1/\overline{l}+ \overline{l}\, {{\gamma }_{\rm P}}^{\prime \prime}(0+)]/2]$ . Formally extending this to the Poisson mosaic case yields a correct result $[\varphi (0) = [1/\overline{l}+ \overline{l} /{{(\overline{l})}^2}]/2 = 1/\overline{l}]$ .

However, the author does not know of any attempt to trace back the Poisson mosaic case to a superimposition of simple grain shapes with a DLM. The parameters d, $[\overline{l}]$ and $[\tau]$ can be determined from the functions P₁, I or g. The interpretation of the function $[g(r)\simeq \gamma ^{\prime \prime}(r)]$ should confirm the parameter values estimated in reciprocal space. The parameter $[\tau]$ is simpler to obtain than any PP parameter. The smaller the ratios $[\tau /d]$ or $[\tau /\overline{l}]$ , the better the extraction of the PP parameters d, $[\overline{l}]$ of the specific model from the approximations $[d\simeq 2\pi /{h_{\rm s}}]$ , $[\overline{l}\simeq 2\pi /{h_{\rm s}}]$ . There are many possibilities for modifying the model and adapting it to special materials. For example, for porous materials other grain shapes can be introduced. The scattering of a large class of tightly packed two-phase systems can be described.

APPENDIX A

Characteristic parameters

The parameters l_p and v_c are connected with the moments M_1,4 of g(r), l_p = M₁ and $[v_{\rm c} = \pi M_4/(3 l_{\rm p})]$ . Operating with equation (4),

$[\eqalignno{l_{\rm p} =\ &\int\limits _{0}^{L}r\, g(r) \,{\rm d} r = \int\limits _{0}^{L}r\, \Big[{{1}\over{2 \pi}}\int\limits _{-\infty }^{\infty }{\exp(-i t r)}\, Q(t)\,{\rm d} t\Big]d r\cr =\ & {{1}\over{2 \pi}}\int\limits _{-\infty }^{\infty }\Big[\int\limits _{0}^{L}r\, {\exp(-i t r)}\,{\rm d} r\Big]\, Q(t)\,{\rm d} t &(9)}]$

is obtained. After changing the order of the integration, d r d t = d t d r, of equation (9), the d r integration leads to a function P(t,L),

$[P(t,L) = \textstyle\int\limits _{0}^{L}r\exp(-i t r) \,{\rm d} r. \eqno (10)]$

Thus, l_p results from

$[l_{\rm p} = {{1}\over{2 \pi }}\int\limits _{-\infty }^{\infty }P(t,L)\, Q(t) \,{\rm d} t. \eqno (11)]$

By an analogous procedure, based on the connection between v_c and M₄,

$[\eqalignno { v_{\rm c} & = {{\pi}\over{3l_{\rm p}}} \int\limits _0^L r^4\, g(r) \, {\rm d} r = {{1}\over{2\pi}} \, {{\pi}\over{3l_p}} \int\limits _{-\infty} ^\infty \Big[\int\limits _0^Lr^4\exp(-i t r) \, {\rm d} r\Big]\, Q(t) \, {\rm d} t, \cr v_{\rm c} & = {{ 1}\over{2 \pi}} \, {{\pi}\over{3l_p}}\int\limits _{-\infty} ^\infty V(t,L)\, Q(t) \, {\rm d} t, \quad V(t,L) = \int\limits _0^Lr^4\exp(-i t r) \, {\rm d} r, & (12) }]$

$[v_{\rm c} = {{1}\over{6 {l_{\rm p}}}}\int\limits _{-\infty }^{\infty } V(t,L) \, Q(t) \, {\rm d} t \eqno (13)]$

results. The terms P(t,L) and V(t,L) are defined by equations (14) and (15):

$[P(t,L) = {{\exp(-i Lt)(1+iLt)-1}\over{t^2}}, \eqno (14)]$

$[V(t,L) = {{\exp(-i Lt)(24i - 24Lt - 12iL^{2}t^{2} + 4L^3 t^3+i L^4 t^4)-24i}\over{t^5}}. \eqno (15)]$

In this way, l_p and v_c are directly traced back to a fixed range order L and to Q(t). Finally, the connection down to the CLDs is defined by equations (1)–(3). A simpler approach to determine $[l_{\rm p}(L,\varphi, f)]$ and $[v_{\rm c}(L,\varphi,f)]$ does not seem to exist.

APPENDIX B

Scattering intensity

The normalized SAS intensity, I(0) = 1, results from a combination of equations (4) and (5):

$[I(h) = {{4\pi}\over{v_{\rm c} \, l_{\rm p}}} {{1}\over{2\pi}}\! \int\limits _{-\infty} ^{\infty} \! \Big[\int\limits _{0}^{L}\exp(-itr) \, {{2-2 \cos(h r)-h r \sin(h r)}\over{h^4}} \,{\rm d} r \Big]\, Q(t)\, {\rm d} t. \eqno (16)]$

After replacing the inner integral by a function T(h,L,t), from equation (16),

$[I(h) = {{2}\over{v_{\rm c}\, l_{\rm p}}} \int\limits _{-\infty}^{\infty} T(h,L,t)\, Q(t) \, {\rm d}t \eqno (17)]$

follows. If $[h \neq \pm t]$ , the term T(h,L,t) is defined by

$[\eqalignno { T(h,L,t) = \ & {{\exp(-iLt)}\over{{h^4 t}{{(h^2-t^2)}^2}}}\bigg \{h t\big[(i L t-3)h^2+{t^2}(1-i L t) \big] \sin(h L) \cr & + 2i \big [(h^2-t^2)^2 - h^4 e^{i L t} \big] \cr &+ t\big[L {h^4}+t(4 i -L t){h^2}-2 i {t^3}\big]\cos(h L)\bigg\} . & (18) }]$

In the limiting case $[h = \pm t]$ , from equation (18),

$[T(t,L,t) = {{{\exp(-2 i L t)}(16 i{e^{i L t}}+2 L t-5i)}\over{8 t^5}}+{{i(2 {L^2} {t^2}+8 i L t-11)}\over{8 {t^5}}} \eqno (19)]$

results. Equations (17)–(19) fix a normalized intensity function I(h) in terms of Q(t) and L.

Acknowledgements

The author cordially thanks the reviewers for critically reading through the manuscript and for their useful hints. Critical points raised by the reviewers helped to improve the manuscript.

References

Burger, C. & Ruland, W. (2001). Acta Cryst. A57, 482–491. Web of Science CrossRef CAS IUCr Journals
Chen, S.-H., Chang, S.-L. & Strey, R. (1991). J. Appl. Cryst. 24, 721–731. CrossRef CAS Web of Science IUCr Journals
Cox, D. R. (1963). Renewal Theory. New York: John Wiley.
Debye, P., Anderson, H. R. & Brumberger, H. (1957). J. Appl. Phys. 28, 679–683. CrossRef CAS Web of Science
Feigin, L. A. & Svergun, D. I. (1987). Structure Analysis by Small-Angle X-ray and Neutron Scattering. New York: Plenum Press.
Gille, W. (2002). Waves Random Media, 12, 85–97. Web of Science CrossRef
Gille, W. (2003). J. Appl. Cryst. 36, 1356–1360. Web of Science CrossRef CAS IUCr Journals
Gille, W. (2005). J. Appl. Cryst. 38, 520–527. Web of Science CrossRef CAS IUCr Journals
Hermann, H. (1991). Stochastic Models of Heterogeneous Materials. Brookfield: Trans Tech Publications.
Levitz, P. & Tchoubar, D. (1992). J. Phys. II France, 2, 771–790. CrossRef CAS
Mazzolo, A., Roesslinger, B. & Gille, W. (2005). J. Math. Phys. 44, 6195–6209. Web of Science CrossRef
Méring, J. & Tchoubar, D. (1968). J. Appl. Cryst. 1, 153–165. CrossRef IUCr Journals
Porod, G. (1952a). Kolloid-Z. 125, 51–57. CrossRef CAS Web of Science
Porod, G. (1952b). Kolloid-Z. 125, 108–122. CrossRef Web of Science
Serra, J. (1982). Image Analysis and Mathematical Morphology. London: Academic Press.
Stoyan, D., Kendall, W. S. & Mecke, J. (1995). Stochastic Geometry and Its Applications. Chichester: John Wiley.
Torquato, S. (2002). Random Heterogeneous Materials. New York: Springer.
Weil, W. (2004). Random Sets. Course on Stochastic Geometry, Martina Franca, Italy, September (2004), pp. 1–50. Mathematisches Institut II, Universitaet Karlsruhe, Germany.

© International Union of Crystallography. Prior permission is not required to reproduce short quotations, tables and figures from this article, provided the original authors and source are cited. For more information, click here.

JOURNAL OF
APPLIED
CRYSTALLOGRAPHY

ISSN: 1600-5767

Volume 40| Part s1| April 2007| Pages s691-s695

doi:10.1107/S0021889806055130