Ordered arrays of cylinders, known as rod packings, are now widely used in descriptions of crystalline structures. These are generalized to include crystallographic packed arrays of filaments with circular cross sections, including curvilinear cylinders whose central axes are generic helices. A suite of the simplest such general rod packings is constructed by projecting line patterns in the hyperbolic plane (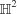 ) onto cubic genus-3 triply periodic minimal surfaces in Euclidean space (
) onto cubic genus-3 triply periodic minimal surfaces in Euclidean space (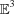 ): the primitive, diamond and gyroid surfaces. The simplest designs correspond to `classical' rod packings containing conventional cylindrical filaments. More complex packings contain three-dimensional arrays of mutually entangled filaments that can be infinitely extended or finite loops forming three-dimensional weavings. The concept of a canonical `ideal' embedding of these weavings is introduced, generalized from that of knot embeddings and found algorithmically by tightening the weaving to minimize the filament length to volume ratio. The tightening algorithm builds on the SONO algorithm for finding ideal conformations of knots. Three distinct classes of weavings are described.
): the primitive, diamond and gyroid surfaces. The simplest designs correspond to `classical' rod packings containing conventional cylindrical filaments. More complex packings contain three-dimensional arrays of mutually entangled filaments that can be infinitely extended or finite loops forming three-dimensional weavings. The concept of a canonical `ideal' embedding of these weavings is introduced, generalized from that of knot embeddings and found algorithmically by tightening the weaving to minimize the filament length to volume ratio. The tightening algorithm builds on the SONO algorithm for finding ideal conformations of knots. Three distinct classes of weavings are described.
Keywords: periodic entanglements; filaments; tangles; hyperbolic tilings; ideal knots; tight knots; weavings; enumeration of tilings; surfaces; rod packing; helices.
Supporting information
Text file https://doi.org/10.1107/S0108767313001682/eo5020sup1.txt |

 journal menu
journal menu











