The information which can be obtained about the shape of crystal atoms by X-ray diffraction is studied in light of a model calculation. The electron density of an atom is treated as a Fourier invariant expansion in terms of harmonic oscillator wavefunctions adapted to the crystal symmetry. Definite limits for the observability of the terms are set by the experimental cutoff in sin θ/λ, and by the volume of the atom. As a consequence, details smaller than a critical size cannot be seen either in the electron density or in the atomic factor. Experimental errors are such that the atomic factor rather than the electron density reveals the significant deformations. Termination effects are studied in a model crystal: deformations are inserted and a truncated set of structure amplitudes is analysed. Here series were used for the radial coefficients 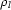 , fl in the harmonic expansions Σ
, fl in the harmonic expansions Σ (r)lK(θ, φ) and Σfl(b)Kl(θ, φ) for the electron density and the scattering factor of a sphere. The radial scattering factors are well reproduced up to the cutoff value of the reciprocal vector, while a fair representation of the radial densities can be reached only by a long series. The termination does not significantly mix components with different angular behaviour. Reasonable contributions from neighbouring atoms have no major effect on the radial scattering factors or densities. Therefore the factors fl calculated for a slightly `too large' sphere will lead to a proper interpretation of the electron distribution in terms of deformed atoms.
(r)lK(θ, φ) and Σfl(b)Kl(θ, φ) for the electron density and the scattering factor of a sphere. The radial scattering factors are well reproduced up to the cutoff value of the reciprocal vector, while a fair representation of the radial densities can be reached only by a long series. The termination does not significantly mix components with different angular behaviour. Reasonable contributions from neighbouring atoms have no major effect on the radial scattering factors or densities. Therefore the factors fl calculated for a slightly `too large' sphere will lead to a proper interpretation of the electron distribution in terms of deformed atoms.

 journal menu
journal menu











