Willis treatment of anharmonic temperature factors including up to fourth-order terms has been generalized and incorporated into a conventional full-matrix least-squares program. The temperature factor T(S) including the anharmonic vibration effect is formulated in the general case using Willis's method. T(S) is based on the Cartesian coordinates defined by the three principal axes of the harmonic thermal ellipsoid. The simultaneous refinement of the parameters in T(S) with the conventional parameters in crystallography, which are based on the crystal lattice system, is possible. In order to introduce T(S) into conventional full-matrix least-squares programs, some other relations were also derived, such as that between crystallographic symmetry and T(S), and that among parameters due to point symmetry of the atom, and so on. The present method was applied to the K and two F atoms in KCuF3 crystals at 296 K with the point symmetries of the sites 422, 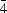 2m and mm2, respectively, and Al and O atoms in α-Al2O3 crystals at 2170 K with the point symmetries 3 and 2, respectively. The features of the potentials of atoms in KCuF3 crystals correspond very well to the peaks on the difference-Fourier maps. After the correction for anharmonic vibration, the difference-Fourier map around each atom became flat. It indicates that in an accurate electron density study the anharmonic vibration effect is not negligible and the Willis method works effectively.
2m and mm2, respectively, and Al and O atoms in α-Al2O3 crystals at 2170 K with the point symmetries 3 and 2, respectively. The features of the potentials of atoms in KCuF3 crystals correspond very well to the peaks on the difference-Fourier maps. After the correction for anharmonic vibration, the difference-Fourier map around each atom became flat. It indicates that in an accurate electron density study the anharmonic vibration effect is not negligible and the Willis method works effectively.

 journal menu
journal menu











