The previous theory of X-ray diffraction in crystals with anisotropic X-ray susceptibility [Dmitrienko (1983). Acta Cryst. A39, 29-35] is applied to cubic crystals. Such a theory is needed if the X-ray wavelengths are near the absorption edges because in this case the X-ray susceptibility may be anisotropic. The most general form of the spatially dependent tensor of X-ray susceptibility is obtained for all cubic space groups. This tensor is anisotropic at any point of a unit cell except those with cubic point symmetry (being averaged over a unit cell the tensor becomes isotropic providing the macro- scopic isotropy of cubic crystals). From the tensor of susceptibility the structure amplitudes and new extinction rules are derived for the glide-plane and screw-axis forbidden reflections (such reflections are forbidden if the susceptibility is isotropic). For example, the hhh forbidden reflections remain extinguished even if the anisotropy is taken into account. Further restrictions on the structure amplitudes of forbidden reflections are obtained with the natural assumption that the anisotropy of susceptibility is localized at the special atomic positions. The tensor form of the structure amplitudes of nonforbidden reflections is also discussed. The general methods are illustrated by their application to the A15 structure (space group Pm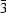 n).
n).

 journal menu
journal menu











