Two congruent lattices are considered, which are misoriented in such a way that they have a fraction 1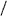 Σ of symmetry translations in common. Whereas for cubic lattices body or face centring does not affect the `multiplicity' or `twin index' Σ, this is not generally true for tetragonal lattices. Consider a fixed misorientation and let ΣP and ΣI be the multiplicities for tP and tI lattices with the same axial ratio c
Σ of symmetry translations in common. Whereas for cubic lattices body or face centring does not affect the `multiplicity' or `twin index' Σ, this is not generally true for tetragonal lattices. Consider a fixed misorientation and let ΣP and ΣI be the multiplicities for tP and tI lattices with the same axial ratio c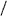 a. Grimmer [Mater. Sci. Forum (1993), 126–128, 269–272] has given an explicit formula for ΣP (depending on the misorientation and the axial ratio) and showed that ΣI = ΣP
a. Grimmer [Mater. Sci. Forum (1993), 126–128, 269–272] has given an explicit formula for ΣP (depending on the misorientation and the axial ratio) and showed that ΣI = ΣP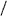 2, ΣP or 2ΣP. Here stronger results on the occurrence of the three possibilities are presented. Lists of all axial ratios c
2, ΣP or 2ΣP. Here stronger results on the occurrence of the three possibilities are presented. Lists of all axial ratios c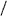 a of tP and tI lattices admitting misorientations with Σ ≤ 5 are given. For each of these misorientations, the twin mirror planes and their normals are listed, so that a synopsis of all possible twin laws of tetragonal crystals by reticular merohedry with Σ ≤ 5 is obtained. It is shown that the two twin laws observed in β-Sn can be described by reticular pseudomerohedry with ΣI = 2 and obliquity δ = 2.6134°.
a of tP and tI lattices admitting misorientations with Σ ≤ 5 are given. For each of these misorientations, the twin mirror planes and their normals are listed, so that a synopsis of all possible twin laws of tetragonal crystals by reticular merohedry with Σ ≤ 5 is obtained. It is shown that the two twin laws observed in β-Sn can be described by reticular pseudomerohedry with ΣI = 2 and obliquity δ = 2.6134°.

 journal menu
journal menu











