The title compound, caesium lanthanum tetrametaphosphate, CsLa(PO3)4, was grown using the flux method and its structure determined by single-crystal X-ray diffraction methods. This compound is isostructural with CsNd(PO3)4. The structure is built up from infinite helical chains, (PO3)n, which are connected by isolated LaO8 dodecahedra and irregularly shaped Cs polyhedra. These chains are formed by corner-sharing of PO4 tetrahedra and run along the b axis.
Supporting information
Key indicators
- Single-crystal X-ray study
- T = 293 K
- Mean
![[sigma]](//journals.iucr.org/logos/entities/sigma_rmgif.gif) (P-O) = 0.005 Å
(P-O) = 0.005 Å
- R factor = 0.022
- wR factor = 0.049
- Data-to-parameter ratio = 12.6
checkCIF/PLATON results
No syntax errors found
 Alert level B
PLAT220_ALERT_2_B Large Non-Solvent O Ueq(max)/Ueq(min) ... 3.61 Ratio
PLAT241_ALERT_2_B Check High U(eq) as Compared to Neighbors .... O10
Alert level B
PLAT220_ALERT_2_B Large Non-Solvent O Ueq(max)/Ueq(min) ... 3.61 Ratio
PLAT241_ALERT_2_B Check High U(eq) as Compared to Neighbors .... O10
 Alert level C
PLAT242_ALERT_2_C Check Low U(eq) as Compared to Neighbors .... P3
PLAT242_ALERT_2_C Check Low U(eq) as Compared to Neighbors .... P4
Alert level C
PLAT242_ALERT_2_C Check Low U(eq) as Compared to Neighbors .... P3
PLAT242_ALERT_2_C Check Low U(eq) as Compared to Neighbors .... P4
 Alert level G
REFLT03_ALERT_4_G WARNING: Large fraction of Friedel related reflns may
be needed to determine absolute structure
From the CIF: _diffrn_reflns_theta_max 28.04
From the CIF: _reflns_number_total 2073
Count of symmetry unique reflns 1503
Completeness (_total/calc) 137.92%
TEST3: Check Friedels for noncentro structure
Estimate of Friedel pairs measured 570
Fraction of Friedel pairs measured 0.379
Are heavy atom types Z>Si present yes
Alert level G
REFLT03_ALERT_4_G WARNING: Large fraction of Friedel related reflns may
be needed to determine absolute structure
From the CIF: _diffrn_reflns_theta_max 28.04
From the CIF: _reflns_number_total 2073
Count of symmetry unique reflns 1503
Completeness (_total/calc) 137.92%
TEST3: Check Friedels for noncentro structure
Estimate of Friedel pairs measured 570
Fraction of Friedel pairs measured 0.379
Are heavy atom types Z>Si present yes
0 ALERT level A = In general: serious problem
2 ALERT level B = Potentially serious problem
2 ALERT level C = Check and explain
1 ALERT level G = General alerts; check
0 ALERT type 1 CIF construction/syntax error, inconsistent or missing data
4 ALERT type 2 Indicator that the structure model may be wrong or deficient
0 ALERT type 3 Indicator that the structure quality may be low
1 ALERT type 4 Improvement, methodology, query or suggestion
Data collection: SMART (Bruker, 1997); cell refinement: SMART; data reduction: SAINT (Bruker, 1997); program(s) used to solve structure: SHELXTL (Bruker, 1997); program(s) used to refine structure: SHELXTL; molecular graphics: SHELXTL; software used to prepare material for publication: SHELXTL.
Crystal data top
| CsLa(PO3)4 | F(000) = 536 |
| Mr = 587.70 | Dx = 3.341 Mg m−3 |
| Monoclinic, P21 | Mo Kα radiation, λ = 0.71073 Å |
| Hall symbol: P 2yb | Cell parameters from 961 reflections |
| a = 7.218 (3) Å | θ = 3.2–28.0° |
| b = 9.254 (3) Å | µ = 7.33 mm−1 |
| c = 8.864 (3) Å | T = 293 K |
| β = 99.377 (5)° | Prism, colorless |
| V = 584.2 (4) Å3 | 0.14 × 0.06 × 0.04 mm |
| Z = 2 | |
Data collection top
Bruker SMART CCD area-detector
diffractometer | 2073 independent reflections |
| Radiation source: fine-focus sealed tube | 1993 reflections with I > 2σ(I) |
| Graphite monochromator | Rint = 0.023 |
| φ and ω scans | θmax = 28.0°, θmin = 2.3° |
Absorption correction: multi-scan
(SADABS; Bruker, 1999) | h = −9→9 |
| Tmin = 0.453, Tmax = 0.746 | k = −12→8 |
| 3731 measured reflections | l = −10→11 |
Refinement top
| Refinement on F2 | Secondary atom site location: difference Fourier map |
| Least-squares matrix: full | w = 1/[σ2(Fo2) + (0.0197P)2 + 0.0183P]
where P = (Fo2 + 2Fc2)/3 |
| R[F2 > 2σ(F2)] = 0.022 | (Δ/σ)max < 0.001 |
| wR(F2) = 0.049 | Δρmax = 1.25 e Å−3 |
| S = 1.02 | Δρmin = −0.72 e Å−3 |
| 2073 reflections | Extinction correction: SHELXL97, Fc*=kFc[1+0.001xFc2λ3/sin(2θ)]-1/4 |
| 164 parameters | Extinction coefficient: 0.0191 (8) |
| 1 restraint | Absolute structure: Flack (1983) |
| Primary atom site location: structure-invariant direct methods | Absolute structure parameter: 0.006 (16) |
Special details top
Geometry. All e.s.d.'s (except the e.s.d. in the dihedral angle between two l.s. planes)
are estimated using the full covariance matrix. The cell e.s.d.'s are taken
into account individually in the estimation of e.s.d.'s in distances, angles
and torsion angles; correlations between e.s.d.'s in cell parameters are only
used when they are defined by crystal symmetry. An approximate (isotropic)
treatment of cell e.s.d.'s is used for estimating e.s.d.'s involving l.s.
planes. |
Refinement. Refinement of F2 against ALL reflections. The weighted R-factor
wR and goodness of fit S are based on F2, conventional
R-factors R are based on F, with F set to zero for
negative F2. The threshold expression of F2 >
σ(F2) is used only for calculating R-factors(gt) etc.
and is not relevant to the choice of reflections for refinement.
R-factors based on F2 are statistically about twice as large
as those based on F, and R- factors based on ALL data will be
even larger. |
Fractional atomic coordinates and isotropic or equivalent isotropic displacement parameters (Å2) top| | x | y | z | Uiso*/Ueq | |
| La1 | 0.20222 (4) | −0.09932 (3) | 0.30272 (3) | 0.00782 (9) | |
| Cs1 | 0.32599 (7) | 0.06604 (4) | −0.17489 (6) | 0.03065 (13) | |
| P1 | 0.9168 (2) | 0.17812 (16) | 0.07312 (16) | 0.0095 (3) | |
| P2 | 0.69456 (19) | −0.02300 (16) | 0.22824 (17) | 0.0105 (3) | |
| P3 | 0.6474 (2) | 0.02504 (15) | 0.54399 (17) | 0.0102 (3) | |
| P4 | 0.9393 (2) | −0.20722 (15) | 0.62514 (17) | 0.0118 (3) | |
| O1 | 0.8567 (6) | 0.2511 (5) | −0.0743 (5) | 0.0190 (9) | |
| O2 | 0.9607 (6) | 0.3021 (4) | 0.1993 (5) | 0.0179 (9) | |
| O3 | 1.0737 (5) | 0.0722 (5) | 0.0894 (5) | 0.0124 (8) | |
| O4 | 0.7305 (5) | 0.1060 (4) | 0.1170 (5) | 0.0161 (9) | |
| O5 | 0.4950 (5) | −0.0665 (5) | 0.1825 (5) | 0.0170 (10) | |
| O6 | 0.8433 (5) | −0.1333 (4) | 0.2329 (5) | 0.0181 (9) | |
| O7 | 0.7231 (6) | 0.0573 (5) | 0.3886 (5) | 0.0191 (9) | |
| O8 | 0.4626 (6) | −0.0448 (5) | 0.5110 (5) | 0.0229 (10) | |
| O9 | 0.6624 (8) | 0.1584 (5) | 0.6349 (6) | 0.0297 (12) | |
| O10 | 0.7875 (7) | −0.0875 (7) | 0.6333 (6) | 0.0442 (15) | |
| O11 | 0.8521 (8) | −0.3499 (5) | 0.5941 (5) | 0.0292 (12) | |
| O12 | 1.0770 (6) | −0.1512 (5) | 0.5349 (5) | 0.0257 (11) | |
Atomic displacement parameters (Å2) top| | U11 | U22 | U33 | U12 | U13 | U23 |
| La1 | 0.00746 (13) | 0.00934 (14) | 0.00701 (13) | 0.00021 (12) | 0.00226 (9) | −0.00030 (12) |
| Cs1 | 0.0372 (3) | 0.0235 (2) | 0.0360 (3) | −0.00028 (17) | 0.0202 (2) | −0.00060 (18) |
| P1 | 0.0117 (6) | 0.0108 (6) | 0.0064 (6) | −0.0004 (5) | 0.0023 (5) | 0.0008 (5) |
| P2 | 0.0093 (7) | 0.0132 (7) | 0.0095 (7) | −0.0018 (5) | 0.0029 (5) | 0.0009 (5) |
| P3 | 0.0102 (7) | 0.0105 (7) | 0.0099 (7) | −0.0002 (5) | 0.0015 (5) | −0.0014 (5) |
| P4 | 0.0128 (7) | 0.0120 (7) | 0.0109 (7) | 0.0013 (5) | 0.0031 (6) | 0.0039 (5) |
| O1 | 0.026 (2) | 0.018 (2) | 0.013 (2) | −0.0003 (18) | 0.0039 (18) | 0.0034 (17) |
| O2 | 0.026 (2) | 0.012 (2) | 0.014 (2) | 0.0044 (16) | −0.0011 (18) | −0.0059 (16) |
| O3 | 0.0119 (19) | 0.016 (2) | 0.0096 (19) | 0.0023 (17) | 0.0032 (15) | 0.0031 (16) |
| O4 | 0.013 (2) | 0.020 (2) | 0.017 (2) | 0.0024 (16) | 0.0068 (17) | 0.0113 (17) |
| O5 | 0.0110 (18) | 0.030 (3) | 0.0098 (19) | −0.0041 (15) | 0.0018 (16) | −0.0028 (15) |
| O6 | 0.0135 (18) | 0.018 (3) | 0.024 (2) | 0.0006 (15) | 0.0082 (17) | 0.0008 (16) |
| O7 | 0.019 (2) | 0.023 (2) | 0.017 (2) | −0.0119 (18) | 0.0083 (18) | −0.0089 (18) |
| O8 | 0.0101 (19) | 0.044 (3) | 0.014 (2) | −0.0112 (18) | 0.0007 (17) | −0.0029 (19) |
| O9 | 0.051 (3) | 0.018 (2) | 0.022 (2) | −0.015 (2) | 0.011 (2) | −0.0112 (19) |
| O10 | 0.042 (3) | 0.060 (4) | 0.035 (3) | 0.039 (3) | 0.018 (2) | 0.014 (3) |
| O11 | 0.048 (3) | 0.019 (2) | 0.016 (2) | −0.018 (2) | −0.009 (2) | 0.0059 (18) |
| O12 | 0.024 (2) | 0.036 (3) | 0.022 (2) | 0.0024 (19) | 0.015 (2) | 0.0106 (19) |
Geometric parameters (Å, º) top
| La1—O12i | 2.426 (4) | P2—O4 | 1.597 (4) |
| La1—O1ii | 2.432 (4) | P3—O8 | 1.468 (4) |
| La1—O8 | 2.463 (4) | P3—O9 | 1.468 (5) |
| La1—O9iii | 2.472 (5) | P3—O10 | 1.573 (5) |
| La1—O3i | 2.526 (4) | P3—O7 | 1.590 (4) |
| La1—O5 | 2.535 (4) | P4—O12 | 1.468 (4) |
| La1—O11iv | 2.537 (5) | P4—O11 | 1.469 (5) |
| La1—O6i | 2.583 (4) | P4—O10 | 1.568 (5) |
| Cs1—O6v | 3.049 (4) | P4—O2viii | 1.608 (4) |
| Cs1—O2ii | 3.186 (4) | O1—La1v | 2.432 (4) |
| Cs1—O3i | 3.193 (4) | O2—P4ix | 1.608 (4) |
| Cs1—O8vi | 3.267 (5) | O2—Cs1v | 3.186 (4) |
| Cs1—O9vi | 3.287 (5) | O3—La1x | 2.526 (4) |
| Cs1—O5 | 3.430 (4) | O3—Cs1x | 3.193 (4) |
| Cs1—O12vii | 3.519 (5) | O5—Cs1ii | 3.642 (4) |
| Cs1—O4 | 3.591 (4) | O6—La1x | 2.583 (4) |
| Cs1—O5v | 3.642 (4) | O6—Cs1ii | 3.049 (4) |
| Cs1—O11v | 3.809 (5) | O8—Cs1xi | 3.267 (5) |
| P1—O1 | 1.473 (4) | O9—La1iv | 2.472 (5) |
| P1—O3 | 1.487 (4) | O9—Cs1xi | 3.287 (5) |
| P1—O2 | 1.597 (4) | O11—La1iii | 2.537 (5) |
| P1—O4 | 1.605 (4) | O11—Cs1ii | 3.809 (5) |
| P2—O6 | 1.477 (4) | O12—La1x | 2.426 (4) |
| P2—O5 | 1.487 (4) | O12—Cs1xii | 3.519 (5) |
| P2—O7 | 1.588 (4) | | |
| | | |
| O12i—La1—O1ii | 123.68 (15) | O2ii—Cs1—O11v | 88.75 (11) |
| O12i—La1—O8 | 75.47 (15) | O3i—Cs1—O11v | 124.74 (11) |
| O1ii—La1—O8 | 138.52 (15) | O8vi—Cs1—O11v | 48.19 (11) |
| O12i—La1—O9iii | 79.58 (16) | O9vi—Cs1—O11v | 66.83 (13) |
| O1ii—La1—O9iii | 71.29 (16) | O5—Cs1—O11v | 170.60 (10) |
| O8—La1—O9iii | 78.02 (18) | O12vii—Cs1—O11v | 49.65 (11) |
| O12i—La1—O3i | 128.10 (14) | O4—Cs1—O11v | 141.94 (10) |
| O1ii—La1—O3i | 75.01 (14) | O5v—Cs1—O11v | 81.70 (10) |
| O8—La1—O3i | 125.08 (15) | O1—P1—O3 | 119.9 (2) |
| O9iii—La1—O3i | 145.15 (15) | O1—P1—O2 | 106.7 (2) |
| O12i—La1—O5 | 146.23 (14) | O3—P1—O2 | 110.2 (2) |
| O1ii—La1—O5 | 76.29 (13) | O1—P1—O4 | 105.6 (2) |
| O8—La1—O5 | 72.77 (13) | O3—P1—O4 | 110.9 (2) |
| O9iii—La1—O5 | 82.90 (15) | O2—P1—O4 | 102.0 (2) |
| O3i—La1—O5 | 80.77 (13) | O6—P2—O5 | 119.2 (2) |
| O12i—La1—O11iv | 76.92 (16) | O6—P2—O7 | 108.1 (3) |
| O1ii—La1—O11iv | 143.28 (15) | O5—P2—O7 | 110.5 (2) |
| O8—La1—O11iv | 71.78 (16) | O6—P2—O4 | 110.1 (2) |
| O9iii—La1—O11iv | 145.42 (16) | O5—P2—O4 | 106.4 (2) |
| O3i—La1—O11iv | 68.82 (14) | O7—P2—O4 | 101.1 (2) |
| O5—La1—O11iv | 103.35 (16) | O8—P3—O9 | 117.6 (3) |
| O12i—La1—O6i | 71.43 (15) | O8—P3—O10 | 107.3 (3) |
| O1ii—La1—O6i | 72.47 (14) | O9—P3—O10 | 107.3 (3) |
| O8—La1—O6i | 144.87 (14) | O8—P3—O7 | 109.8 (2) |
| O9iii—La1—O6i | 106.73 (16) | O9—P3—O7 | 108.2 (3) |
| O3i—La1—O6i | 70.45 (13) | O10—P3—O7 | 106.1 (3) |
| O5—La1—O6i | 141.82 (14) | O12—P4—O11 | 121.5 (3) |
| O11iv—La1—O6i | 89.37 (15) | O12—P4—O10 | 108.4 (3) |
| O6v—Cs1—O2ii | 116.76 (11) | O11—P4—O10 | 111.2 (3) |
| O6v—Cs1—O3i | 81.18 (10) | O12—P4—O2viii | 105.8 (3) |
| O2ii—Cs1—O3i | 67.77 (11) | O11—P4—O2viii | 109.9 (2) |
| O6v—Cs1—O8vi | 108.13 (12) | O10—P4—O2viii | 97.1 (3) |
| O2ii—Cs1—O8vi | 89.11 (11) | P1—O1—La1v | 170.5 (3) |
| O3i—Cs1—O8vi | 156.67 (11) | P1—O2—P4ix | 130.2 (3) |
| O6v—Cs1—O9vi | 89.16 (12) | P1—O2—Cs1v | 116.8 (2) |
| O2ii—Cs1—O9vi | 133.68 (11) | P4ix—O2—Cs1v | 106.90 (18) |
| O3i—Cs1—O9vi | 158.27 (11) | P1—O3—La1x | 131.9 (2) |
| O8vi—Cs1—O9vi | 45.06 (11) | P1—O3—Cs1x | 117.2 (2) |
| O6v—Cs1—O5 | 123.67 (11) | La1x—O3—Cs1x | 110.74 (13) |
| O2ii—Cs1—O5 | 85.29 (10) | P2—O4—P1 | 133.4 (3) |
| O3i—Cs1—O5 | 59.23 (10) | P2—O4—Cs1 | 99.96 (18) |
| O8vi—Cs1—O5 | 124.30 (11) | P1—O4—Cs1 | 118.90 (19) |
| O9vi—Cs1—O5 | 112.67 (12) | P2—O5—La1 | 139.0 (2) |
| O6v—Cs1—O12vii | 104.79 (11) | P2—O5—Cs1 | 109.8 (2) |
| O2ii—Cs1—O12vii | 42.58 (10) | La1—O5—Cs1 | 103.63 (12) |
| O3i—Cs1—O12vii | 105.20 (10) | P2—O5—Cs1ii | 85.81 (18) |
| O8vi—Cs1—O12vii | 52.16 (10) | La1—O5—Cs1ii | 102.61 (13) |
| O9vi—Cs1—O12vii | 96.05 (11) | Cs1—O5—Cs1ii | 112.99 (11) |
| O5—Cs1—O12vii | 122.23 (10) | P2—O6—La1x | 128.2 (2) |
| O6v—Cs1—O4 | 106.49 (10) | P2—O6—Cs1ii | 110.9 (2) |
| O2ii—Cs1—O4 | 124.81 (10) | La1x—O6—Cs1ii | 120.67 (14) |
| O3i—Cs1—O4 | 87.90 (10) | P2—O7—P3 | 132.4 (3) |
| O8vi—Cs1—O4 | 108.88 (10) | P3—O8—La1 | 142.9 (3) |
| O9vi—Cs1—O4 | 76.17 (11) | P3—O8—Cs1xi | 94.7 (2) |
| O5—Cs1—O4 | 41.09 (9) | La1—O8—Cs1xi | 113.81 (14) |
| O12vii—Cs1—O4 | 147.57 (10) | P3—O9—La1iv | 151.2 (3) |
| O6v—Cs1—O5v | 43.81 (10) | P3—O9—Cs1xi | 93.9 (2) |
| O2ii—Cs1—O5v | 160.56 (10) | La1iv—O9—Cs1xi | 114.79 (16) |
| O3i—Cs1—O5v | 104.08 (10) | P4—O10—P3 | 147.3 (4) |
| O8vi—Cs1—O5v | 96.90 (10) | P4—O11—La1iii | 146.8 (3) |
| O9vi—Cs1—O5v | 56.89 (10) | P4—O11—Cs1ii | 115.6 (2) |
| O5—Cs1—O5v | 106.08 (7) | La1iii—O11—Cs1ii | 96.80 (13) |
| O12vii—Cs1—O5v | 131.32 (10) | P4—O12—La1x | 155.6 (3) |
| O4—Cs1—O5v | 70.60 (9) | P4—O12—Cs1xii | 96.5 (2) |
| O6v—Cs1—O11v | 65.60 (11) | La1x—O12—Cs1xii | 106.89 (15) |
| Symmetry codes: (i) x−1, y, z; (ii) −x+1, y−1/2, −z; (iii) −x+1, y−1/2, −z+1; (iv) −x+1, y+1/2, −z+1; (v) −x+1, y+1/2, −z; (vi) x, y, z−1; (vii) x−1, y, z−1; (viii) −x+2, y−1/2, −z+1; (ix) −x+2, y+1/2, −z+1; (x) x+1, y, z; (xi) x, y, z+1; (xii) x+1, y, z+1. |

 journal menu
journal menu




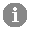






 Alert level B
Alert level B
 Alert level C
Alert level C
 Alert level G
Alert level G



