Supporting information
Crystallographic Information File (CIF) https://doi.org/10.1107/S1600536801014672/bt6081sup1.cif | |
Structure factor file (CIF format) https://doi.org/10.1107/S1600536801014672/bt6081Isup2.hkl |
CCDC reference: 175353
Key indicators
- Single-crystal X-ray study
- T = 293 K
- Mean
![[sigma]](https://journals.iucr.org/logos/entities/sigma_rmgif.gif) (C-C) = 0.003 Å
(C-C) = 0.003 Å - R factor = 0.038
- wR factor = 0.190
- Data-to-parameter ratio = 12.3
checkCIF results
No syntax errors found ADDSYM reports no extra symmetry
Colorless needle-shaped single crystals of (I) were grown from a saturated aqueous solution containing β-alanine and maleic acid in stoichiometric ratio.
All the H atoms were generated geometrically and were allowed to ride on their respective parent atoms with SHELXL97 (Sheldrick, 1997) defaults for bond lengths and displacement parameters. The torsion angles about the C—O bonds of the two hydroxyl groups were refined.
Data collection: Enraf-Nonius CAD-4; cell refinement: CAD-4 Software (Enraf-Nonius, 1989); data reduction: CAD-4 Software; program(s) used to solve structure: SHELXS97 (Sheldrick, 1990); program(s) used to refine structure: SHELXL97 (Sheldrick, 1997); molecular graphics: PLATON (spek, 1999); software used to prepare material for publication: SHELXL97.
![[Figure 1]](https://journals.iucr.org/e/issues/2001/10/00/bt6081/bt6081fig1thm.gif)
| Fig. 1. The molecular structure of (I) with the atom-numbering scheme and 50% probability displacement ellipsoids. |
![[Figure 2]](https://journals.iucr.org/e/issues/2001/10/00/bt6081/bt6081fig2thm.gif)
| Fig. 2. Packing of the molecules of (I) viewed down the a axis. |
| C3H8NO2+·C4H3O4− | F(000) = 432 |
| Mr = 205.17 | Dx = 1.492 Mg m−3 Dm = 1.51 Mg m−3 Dm measured by flotation in mixture of xylene and carbon tetrachloride |
| Monoclinic, P21/n | Mo Kα radiation, λ = 0.71073 Å |
| a = 5.4186 (11) Å | Cell parameters from 25 reflections |
| b = 22.951 (5) Å | θ = 6–17° |
| c = 7.4518 (15) Å | µ = 0.13 mm−1 |
| β = 99.730 (16)° | T = 293 K |
| V = 913.4 (3) Å3 | Needle, colorless |
| Z = 4 | 0.35 × 0.30 × 0.15 mm |
| Enraf-Nonius CAD-4 diffractometer | 1344 reflections with I > 2σ(I) |
| Radiation source: fine-focus sealed tube | Rint = 0.019 |
| Graphite monochromator | θmax = 25.0°, θmin = 2.9° |
| ω–2θ scans | h = 0→6 |
| Absorption correction: ψ scan (North et al., 1968) | k = 0→27 |
| Tmin = 0.97, Tmax = 0.99 | l = −8→8 |
| 1775 measured reflections | 2 standard reflections every 200 reflections |
| 1600 independent reflections | intensity decay: <2% |
| Refinement on F2 | Secondary atom site location: difference Fourier map |
| Least-squares matrix: full | Hydrogen site location: inferred from neighbouring sites |
| R[F2 > 2σ(F2)] = 0.038 | H-atom parameters constrained |
| wR(F2) = 0.190 | w = 1/[σ2(Fo2) + (0.1299P)2 + 0.1847P] where P = (Fo2 + 2Fc2)/3 |
| S = 1.16 | (Δ/σ)max < 0.001 |
| 1600 reflections | Δρmax = 0.30 e Å−3 |
| 130 parameters | Δρmin = −0.30 e Å−3 |
| 0 restraints | Extinction correction: SHELXL97, Fc*=kFc[1+0.001xFc2λ3/sin(2θ)]-1/4 |
| Primary atom site location: structure-invariant direct methods | Extinction coefficient: 0.047 (14) |
| C3H8NO2+·C4H3O4− | V = 913.4 (3) Å3 |
| Mr = 205.17 | Z = 4 |
| Monoclinic, P21/n | Mo Kα radiation |
| a = 5.4186 (11) Å | µ = 0.13 mm−1 |
| b = 22.951 (5) Å | T = 293 K |
| c = 7.4518 (15) Å | 0.35 × 0.30 × 0.15 mm |
| β = 99.730 (16)° |
| Enraf-Nonius CAD-4 diffractometer | 1344 reflections with I > 2σ(I) |
| Absorption correction: ψ scan (North et al., 1968) | Rint = 0.019 |
| Tmin = 0.97, Tmax = 0.99 | 2 standard reflections every 200 reflections |
| 1775 measured reflections | intensity decay: <2% |
| 1600 independent reflections |
| R[F2 > 2σ(F2)] = 0.038 | 0 restraints |
| wR(F2) = 0.190 | H-atom parameters constrained |
| S = 1.16 | Δρmax = 0.30 e Å−3 |
| 1600 reflections | Δρmin = −0.30 e Å−3 |
| 130 parameters |
Geometry. All e.s.d.'s (except the e.s.d. in the dihedral angle between two l.s. planes) are estimated using the full covariance matrix. The cell e.s.d.'s are taken into account individually in the estimation of e.s.d.'s in distances, angles and torsion angles; correlations between e.s.d.'s in cell parameters are only used when they are defined by crystal symmetry. An approximate (isotropic) treatment of cell e.s.d.'s is used for estimating e.s.d.'s involving l.s. planes. |
Refinement. Refinement of F2 against ALL reflections. The weighted R-factor wR and goodness of fit S are based on F2, conventional R-factors R are based on F, with F set to zero for negative F2. The threshold expression of F2 > σ(F2) is used only for calculating R-factors(gt) etc. and is not relevant to the choice of reflections for refinement. R-factors based on F2 are statistically about twice as large as those based on F, and R- factors based on ALL data will be even larger. |
| x | y | z | Uiso*/Ueq | ||
| O1 | 0.9600 (3) | 0.65798 (8) | 0.9827 (3) | 0.0496 (6) | |
| H1 | 0.8833 | 0.6312 | 1.0209 | 0.074* | |
| O2 | 0.5884 (4) | 0.70108 (8) | 0.9471 (3) | 0.0590 (6) | |
| N1 | 0.9147 (3) | 0.85468 (8) | 0.7698 (3) | 0.0371 (5) | |
| H1A | 0.8328 | 0.8878 | 0.7803 | 0.056* | |
| H1B | 0.9073 | 0.8462 | 0.6525 | 0.056* | |
| H1C | 1.0739 | 0.8587 | 0.8223 | 0.056* | |
| O3 | 0.7870 (3) | 0.04863 (7) | 0.9235 (3) | 0.0475 (6) | |
| H3 | 0.7334 | 0.0178 | 0.8765 | 0.071* | |
| O4 | 0.6457 (4) | 0.13567 (8) | 0.9679 (3) | 0.0504 (6) | |
| O5 | 0.6211 (3) | −0.04031 (7) | 0.7561 (2) | 0.0450 (5) | |
| O6 | 0.2587 (3) | −0.06948 (7) | 0.5973 (2) | 0.0482 (6) | |
| C1 | 0.8066 (4) | 0.70073 (10) | 0.9310 (3) | 0.0378 (6) | |
| C2 | 0.9311 (5) | 0.75014 (10) | 0.8468 (3) | 0.0408 (6) | |
| H2A | 1.1033 | 0.7537 | 0.9078 | 0.049* | |
| H2B | 0.9329 | 0.7414 | 0.7196 | 0.049* | |
| C3 | 0.7980 (5) | 0.80692 (10) | 0.8605 (4) | 0.0421 (6) | |
| H3A | 0.6238 | 0.8029 | 0.8043 | 0.051* | |
| H3B | 0.8030 | 0.8166 | 0.9878 | 0.051* | |
| C4 | 0.6116 (4) | 0.08756 (10) | 0.8980 (3) | 0.0350 (6) | |
| C5 | 0.3642 (4) | 0.07430 (10) | 0.7857 (3) | 0.0374 (6) | |
| H5 | 0.2522 | 0.1053 | 0.7732 | 0.045* | |
| C6 | 0.2744 (4) | 0.02598 (10) | 0.7000 (3) | 0.0373 (6) | |
| H6 | 0.1098 | 0.0286 | 0.6399 | 0.045* | |
| C7 | 0.3957 (4) | −0.03178 (9) | 0.6848 (3) | 0.0339 (6) |
| U11 | U22 | U33 | U12 | U13 | U23 | |
| O1 | 0.0440 (11) | 0.0380 (10) | 0.0668 (12) | 0.0048 (8) | 0.0094 (8) | 0.0142 (8) |
| O2 | 0.0438 (11) | 0.0502 (12) | 0.0876 (15) | 0.0067 (8) | 0.0241 (10) | 0.0223 (10) |
| N1 | 0.0342 (11) | 0.0277 (10) | 0.0491 (12) | 0.0015 (7) | 0.0056 (8) | −0.0011 (8) |
| O3 | 0.0340 (10) | 0.0399 (10) | 0.0657 (12) | 0.0034 (7) | 0.0006 (8) | −0.0109 (8) |
| O4 | 0.0490 (11) | 0.0379 (10) | 0.0603 (11) | −0.0004 (7) | −0.0024 (9) | −0.0136 (8) |
| O5 | 0.0398 (10) | 0.0312 (9) | 0.0624 (12) | 0.0066 (7) | 0.0043 (8) | −0.0059 (7) |
| O6 | 0.0483 (11) | 0.0353 (10) | 0.0600 (11) | −0.0048 (8) | 0.0061 (8) | −0.0129 (8) |
| C1 | 0.0392 (13) | 0.0355 (13) | 0.0392 (12) | 0.0027 (9) | 0.0080 (9) | 0.0009 (9) |
| C2 | 0.0389 (13) | 0.0332 (13) | 0.0518 (14) | 0.0030 (9) | 0.0117 (11) | 0.0041 (10) |
| C3 | 0.0413 (13) | 0.0346 (13) | 0.0536 (14) | 0.0033 (9) | 0.0169 (11) | 0.0032 (10) |
| C4 | 0.0370 (12) | 0.0311 (12) | 0.0375 (11) | −0.0008 (9) | 0.0076 (9) | 0.0004 (9) |
| C5 | 0.0346 (12) | 0.0317 (12) | 0.0457 (12) | 0.0059 (9) | 0.0064 (10) | −0.0034 (9) |
| C6 | 0.0304 (11) | 0.0376 (13) | 0.0430 (12) | 0.0017 (9) | 0.0034 (9) | −0.0032 (10) |
| C7 | 0.0375 (12) | 0.0292 (11) | 0.0366 (11) | −0.0012 (9) | 0.0106 (9) | 0.0008 (9) |
| O1—C1 | 1.301 (3) | C1—C2 | 1.509 (3) |
| O1—H1 | 0.8200 | C2—C3 | 1.501 (3) |
| O2—C1 | 1.209 (3) | C2—H2A | 0.9700 |
| N1—C3 | 1.484 (3) | C2—H2B | 0.9700 |
| N1—H1A | 0.8900 | C3—H3A | 0.9700 |
| N1—H1B | 0.8900 | C3—H3B | 0.9700 |
| N1—H1C | 0.8900 | C4—C5 | 1.487 (3) |
| O3—C4 | 1.295 (3) | C5—C6 | 1.330 (3) |
| O3—H3 | 0.8200 | C5—H5 | 0.9300 |
| O4—C4 | 1.222 (3) | C6—C7 | 1.492 (3) |
| O5—C7 | 1.262 (3) | C6—H6 | 0.9300 |
| O6—C7 | 1.250 (3) | ||
| C1—O1—H1 | 109.5 | N1—C3—H3A | 109.4 |
| C3—N1—H1A | 109.5 | C2—C3—H3A | 109.4 |
| C3—N1—H1B | 109.5 | N1—C3—H3B | 109.4 |
| H1A—N1—H1B | 109.5 | C2—C3—H3B | 109.4 |
| C3—N1—H1C | 109.5 | H3A—C3—H3B | 108.0 |
| H1A—N1—H1C | 109.5 | O4—C4—O3 | 120.4 (2) |
| H1B—N1—H1C | 109.5 | O4—C4—C5 | 118.8 (2) |
| C4—O3—H3 | 109.5 | O3—C4—C5 | 120.7 (2) |
| O2—C1—O1 | 124.2 (2) | C6—C5—C4 | 131.5 (2) |
| O2—C1—C2 | 123.4 (2) | C6—C5—H5 | 114.2 |
| O1—C1—C2 | 112.5 (2) | C4—C5—H5 | 114.2 |
| C3—C2—C1 | 111.7 (2) | C5—C6—C7 | 130.3 (2) |
| C3—C2—H2A | 109.3 | C5—C6—H6 | 114.8 |
| C1—C2—H2A | 109.3 | C7—C6—H6 | 114.8 |
| C3—C2—H2B | 109.3 | O6—C7—O5 | 124.0 (2) |
| C1—C2—H2B | 109.3 | O6—C7—C6 | 115.1 (2) |
| H2A—C2—H2B | 107.9 | O5—C7—C6 | 120.9 (2) |
| N1—C3—C2 | 111.3 (2) | ||
| O2—C1—C2—C3 | 24.6 (4) | O3—C4—C5—C6 | 1.4 (4) |
| O1—C1—C2—C3 | −155.8 (2) | C4—C5—C6—C7 | −1.3 (5) |
| C1—C2—C3—N1 | −177.4 (2) | C5—C6—C7—O6 | 178.3 (2) |
| O4—C4—C5—C6 | −177.7 (3) | C5—C6—C7—O5 | −2.0 (4) |
| D—H···A | D—H | H···A | D···A | D—H···A |
| O1—H1···O6i | 0.82 | 1.71 | 2.522 (3) | 172 |
| N1—H1A···O5ii | 0.89 | 2.00 | 2.880 (3) | 170 |
| N1—H1B···O2iii | 0.89 | 2.23 | 3.012 (3) | 146 |
| N1—H1C···O4iv | 0.89 | 1.99 | 2.823 (3) | 155 |
| O3—H3···O5 | 0.82 | 1.66 | 2.481 (2) | 173 |
| C2—H2B···O2iii | 0.97 | 2.67 | 3.421 (3) | 134 |
| C6—H6···O6v | 0.93 | 2.61 | 3.477 (3) | 156 |
| Symmetry codes: (i) x+1/2, −y+1/2, z+1/2; (ii) x, y+1, z; (iii) x+1/2, −y+3/2, z−1/2; (iv) −x+2, −y+1, −z+2; (v) −x, −y, −z+1. |
Experimental details
| Crystal data | |
| Chemical formula | C3H8NO2+·C4H3O4− |
| Mr | 205.17 |
| Crystal system, space group | Monoclinic, P21/n |
| Temperature (K) | 293 |
| a, b, c (Å) | 5.4186 (11), 22.951 (5), 7.4518 (15) |
| β (°) | 99.730 (16) |
| V (Å3) | 913.4 (3) |
| Z | 4 |
| Radiation type | Mo Kα |
| µ (mm−1) | 0.13 |
| Crystal size (mm) | 0.35 × 0.30 × 0.15 |
| Data collection | |
| Diffractometer | Enraf-Nonius CAD-4 diffractometer |
| Absorption correction | ψ scan (North et al., 1968) |
| Tmin, Tmax | 0.97, 0.99 |
| No. of measured, independent and observed [I > 2σ(I)] reflections | 1775, 1600, 1344 |
| Rint | 0.019 |
| (sin θ/λ)max (Å−1) | 0.594 |
| Refinement | |
| R[F2 > 2σ(F2)], wR(F2), S | 0.038, 0.190, 1.16 |
| No. of reflections | 1600 |
| No. of parameters | 130 |
| H-atom treatment | H-atom parameters constrained |
| Δρmax, Δρmin (e Å−3) | 0.30, −0.30 |
Computer programs: Enraf-Nonius CAD-4, CAD-4 Software (Enraf-Nonius, 1989), CAD-4 Software, SHELXS97 (Sheldrick, 1990), SHELXL97 (Sheldrick, 1997), PLATON (spek, 1999), SHELXL97.
| O1—C1 | 1.301 (3) | O6—C7 | 1.250 (3) |
| O2—C1 | 1.209 (3) | C1—C2 | 1.509 (3) |
| N1—C3 | 1.484 (3) | C2—C3 | 1.501 (3) |
| O3—C4 | 1.295 (3) | C4—C5 | 1.487 (3) |
| O4—C4 | 1.222 (3) | C5—C6 | 1.330 (3) |
| O5—C7 | 1.262 (3) | C6—C7 | 1.492 (3) |
| O2—C1—O1 | 124.2 (2) | O3—C4—C5 | 120.7 (2) |
| O2—C1—C2 | 123.4 (2) | C6—C5—C4 | 131.5 (2) |
| O1—C1—C2 | 112.5 (2) | C5—C6—C7 | 130.3 (2) |
| C3—C2—C1 | 111.7 (2) | O6—C7—O5 | 124.0 (2) |
| N1—C3—C2 | 111.3 (2) | O6—C7—C6 | 115.1 (2) |
| O4—C4—O3 | 120.4 (2) | O5—C7—C6 | 120.9 (2) |
| O4—C4—C5 | 118.8 (2) | ||
| O2—C1—C2—C3 | 24.6 (4) | O3—C4—C5—C6 | 1.4 (4) |
| O1—C1—C2—C3 | −155.8 (2) | C4—C5—C6—C7 | −1.3 (5) |
| C1—C2—C3—N1 | −177.4 (2) | C5—C6—C7—O6 | 178.3 (2) |
| O4—C4—C5—C6 | −177.7 (3) | C5—C6—C7—O5 | −2.0 (4) |
| D—H···A | D—H | H···A | D···A | D—H···A |
| O1—H1···O6i | 0.82 | 1.71 | 2.522 (3) | 172.0 |
| N1—H1A···O5ii | 0.89 | 2.00 | 2.880 (3) | 169.5 |
| N1—H1B···O2iii | 0.89 | 2.23 | 3.012 (3) | 145.9 |
| N1—H1C···O4iv | 0.89 | 1.99 | 2.823 (3) | 155.0 |
| O3—H3···O5 | 0.82 | 1.66 | 2.481 (2) | 172.8 |
| C2—H2B···O2iii | 0.97 | 2.67 | 3.421 (3) | 134.1 |
| C6—H6···O6v | 0.93 | 2.61 | 3.477 (3) | 155.8 |
| Symmetry codes: (i) x+1/2, −y+1/2, z+1/2; (ii) x, y+1, z; (iii) x+1/2, −y+3/2, z−1/2; (iv) −x+2, −y+1, −z+2; (v) −x, −y, −z+1. |

 Subscribe to Acta Crystallographica Section E: Crystallographic Communications
Subscribe to Acta Crystallographica Section E: Crystallographic Communications
The full text of this article is available to subscribers to the journal.
- Information on subscribing
- Sample issue
- If you have already subscribed, you may need to register

 journal menu
journal menu




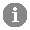








Structural data for complexes of organic acids with amino acids seem to be very limited. Among organic acids, simple carboxylic acids, which are believed to have existed in the prebiotic earth (Miller & Orgel, 1974; Kvenvolden et al., 1971), form crystalline complexes with amino acids. X-ray studies on many such compounds are being carried out in our laboratory with the aim of studying the nature of intermolecular interactions and characteristic aggregation patterns, at atomic resolution. Recently, the crystal structures of glycinium maleate (Rajagopal et al., 2001) and L-alaninium maleate (Alagar et al., 2001) have been reported. The present study reports the crystal structure of β-alaninium maleate, (I), a complex of β-alanine with maleic acid. β-Alanine is the only naturally occurring β-amino acid and is a constituent of the dipeptides carnosine and anserine.
Fig. 1 shows the molecular structure of (I) with the atom-numbering scheme. The β-alanine molecule exists in the cationic form with a positively charged amino group and an uncharged carboxylic acid group. The maleic acid molecule exists in the mono-ionized state. The semi-maleate ion is essentially planar as observed in the crystal structures of similar complexes. In the semi-meleate ion, the intramolecular hydrogen bond between atoms O3 and O5 is found to be asymmetric, as in the crystal structures of maleic acid (James & Williams, 1974), glycinium maleate and L-alaninium maleate. However, in the crystal structures of complexes of maleic acid with DL– and L-arginine (Ravishankar et al., 1998) and L-histidine and L-lysine (Pratap et al., 2000), this intramolecular hydrogen bond between the carboxylic acid and carboxylate groups is symmetric with an H atom shared between the respective O atoms. A common feature observed among the crystal structures of amino acid–maleic acid complexes is that the shortest cell dimension in all of them is close to 5.4 Å, with the exception of lysine–maleic acid complex. It is interesting to note that the shortest cell dimension in almost all the crystal structures of amino acids themselves lie in the neighborhood of 5.4 Å (Suresh & Vijayan, 1983).
Fig. 2 shows the packing of the molecules of (I) viewed down the a axis. The β-alaninium and semi-maleate ions form alternate columns parallel to the axis of intermediate length, as in L-alaninium maleate. The semi-maleate ions do not have direct hydrogen-bonded interactions among themselves. They link the β-alaninium ions into a linear chain running parallel to the longer axis. A head-to-tail hydrogen bond is observed between the n-glide related β-alaninium ions. Strikingly, the cell lengths of (I) are almost similar to those in L-alaninium maleate. However, in (I), β-alaninium interacts with the semi-maleate anion through the ionized carboxylate group, as in glycinium maleate, where as in L-alaninium maleate, the interaction is through the carboxylic acid group. Such differences in the nature of interaction between individual molecules is reflected in the packing mode. The zigzag packing of molecules observed in (I) is distinctly different from those observed in the crystal structures of other amino acid–maleic acid complexes. The crystal packing is also characterized by the presence of two C—H···O hydrogen bonds.