Buy article online - an online subscription or single-article purchase is required to access this article.

Urotropin (U) and azelaic acid (AA) form 1:1 co-crystals (UA) that give rise to a rather complex diffraction pattern, the main features of which are diffuse rods and bands in addition to the Bragg reflections. UA is characterized by solvent inclusions, parasite phases, and high vacancy and dislocation densities. These defects compounded with the pronounced tendency of U to escape from the crystal edifice lead to at least seven exotic phase transitions (many of which barely manifest themselves in a differential scanning calorimetry trace). These involve different incommensurate phases and a peritectoid reaction in the recrystallization regime (
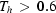
). The system may be understood as an OD (order–disorder) structure based on a layer with layer group
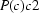
and cell
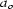
≃ 4.7,
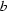
≃ 26.1 and

≃ 14.4 Å. At 338 K the layer stacking is random, but with decreasing temperature the build-up of an orthorhombic MDO (maximal degree of order) structure with cell
a
= 2
a
,
b
=
b,
c
=
c and space group
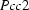
is begun (at ∼301 K). The superposition structure of the OD system at
T = 286 (1) K with space group
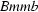
and cell
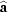
=
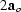
,
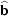
=
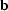
and
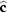
=
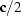
owes its cohesion to van der Waals interactions between the AA chains and to three types of hydrogen bonds of varied strength between U—U and U—AA. Before reaching completion, this MDO structure is transformed, at 282 K, into a monoclinic one with cell
a
= −
a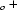 c
c/4,
b
=
b,
c
= −2
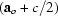
, space group
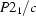
, spontaneous deformation ∼2°, and ferroelastic domains. This transformation is achieved in two steps: first a furtive triggering transition, which is not yet fully understood, and second an improper ferroelastic transition. At ∼233 K, the system reaches its ground state (cell
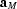
=
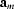
,
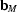
=
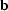
,
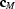
=
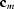
and space group
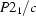
)
via an irreversible transition. The phase transitions below 338 K are described by a model based on the interaction of two thermally activated slip systems. The OD structure is described in terms of a three-dimensional Monte Carlo model that involves first- and second-neighbour interactions along the
a axis and first-neighbour interactions along the
b and
c axes. This model includes random shifts of the chains along their axes and satisfactorily accounts for most features that are seen in the observed diffraction pattern.
Supporting information
CCDC references: 1157222; 1157223; 205167
Data collection: Stoe IPDS; cell refinement: Stoe IPDS; data reduction: Stoe IPDS; program(s) used to solve structure: SHELXS97 (Sheldrick, 1990); program(s) used to refine structure: SHELXL97 (Sheldrick, 1997); molecular graphics: Bruker XP; software used to prepare material for publication: Bruker SHELXTL.
Crystal data top
| (C6H12N4·C9H16O4) | Dx = 1.231 Mg m−3 |
| Mr = 328.41 | Melting point: 403 K |
| Orthorhombic, Bmmb | Mo Kα radiation, λ = 0.71073 Å |
| a = 9.4157 (19) Å | Cell parameters from 721 reflections |
| b = 26.124 (5) Å | θ = 14.5–24.1° |
| c = 7.2034 (14) Å | µ = 0.09 mm−1 |
| V = 1771.9 (6) Å3 | T = 286 K |
| Z = 4 | Platelet, colourless |
| F(000) = 712 | 0.72 × 0.56 × 0.04 mm |
Data collection top
Stoe IPDS
diffractometer | 539 reflections with I > 2σ(I) |
| Radiation source: fine-focus sealed tube | Rint = 0.053 |
| Graphite monochromator | θmax = 25.0°, θmin = 3.6° |
| Detector resolution: 6.67 pixels mm-1 | h = −10→10 |
| φ scans | k = −31→31 |
| 6062 measured reflections | l = −8→8 |
| 818 independent reflections | |
Refinement top
| Refinement on F2 | Primary atom site location: structure-invariant direct methods |
| Least-squares matrix: full | Secondary atom site location: difference Fourier map |
| R[F2 > 2σ(F2)] = 0.041 | Hydrogen site location: inferred from neighbouring sites |
| wR(F2) = 0.126 | H atoms treated by a mixture of independent and constrained refinement |
| S = 0.91 | w = 1/[σ2(Fo2) + (0.0754P)2 + 0.4007P]
where P = (Fo2 + 2Fc2)/3 |
| 818 reflections | (Δ/σ)max < 0.001 |
| 110 parameters | Δρmax = 0.15 e Å−3 |
| 0 restraints | Δρmin = −0.13 e Å−3 |
Special details top
Geometry. All e.s.d.'s (except the e.s.d. in the dihedral angle between two l.s. planes)
are estimated using the full covariance matrix. The cell e.s.d.'s are taken
into account individually in the estimation of e.s.d.'s in distances, angles
and torsion angles; correlations between e.s.d.'s in cell parameters are only
used when they are defined by crystal symmetry. An approximate (isotropic)
treatment of cell e.s.d.'s is used for estimating e.s.d.'s involving l.s.
planes. Authors remarks: Note that the structure is disordered, with the superposition
of two acid chains and splitted carboxylic functions. This leads to
problematic calculations of torsion angles, in the check-CIF procedure. |
Refinement. Refinement of F2 against ALL reflections. The weighted R-factor
wR and goodness of fit S are based on F2, conventional
R-factors R are based on F, with F set to zero for
negative F2. The threshold expression of F2 >
σ(F2) is used only for calculating R-factors(gt) etc.
and is not relevant to the choice of reflections for refinement.
R-factors based on F2 are statistically about twice as large
as those based on F, and R- factors based on ALL data will be
even larger. |
Fractional atomic coordinates and isotropic or equivalent isotropic displacement parameters (Å2) top| | x | y | z | Uiso*/Ueq | Occ. (<1) |
| O1 | 0.5913 (3) | 0.37538 (12) | 0.2149 (4) | 0.0991 (10) | 0.50 |
| H1 | 0.5000 | 0.343 (2) | 0.298 (8) | 0.23 (2)* | |
| O2A | 0.3868 (10) | 0.3719 (5) | 0.0919 (13) | 0.139 (4) | 0.25 |
| O2B | 0.4232 (9) | 0.3570 (3) | 0.0196 (10) | 0.100 (2) | 0.25 |
| N1 | 0.5000 | 0.29636 (7) | 0.4327 (2) | 0.0638 (5) | |
| N2 | 0.62853 (18) | 0.2500 | 0.6708 (2) | 0.0706 (6) | |
| C1 | 0.5000 | 0.38525 (9) | 0.0717 (3) | 0.0717 (7) | |
| C2 | 0.5749 (4) | 0.42167 (13) | −0.0624 (5) | 0.0731 (9) | 0.50 |
| H2A | 0.6151 | 0.4499 | 0.0074 | 0.107 (13)* | 0.50 |
| H2B | 0.6526 | 0.4037 | −0.1222 | 0.108 (13)* | 0.50 |
| C3 | 0.4764 (11) | 0.44274 (12) | −0.2102 (4) | 0.075 (2) | 0.50 |
| H3A | 0.4282 | 0.4146 | −0.2713 | 0.107 (13)* | 0.50 |
| H3B | 0.4049 | 0.4641 | −0.1519 | 0.101 (13)* | 0.50 |
| C4 | 0.5559 (4) | 0.47382 (15) | −0.3530 (5) | 0.0865 (12) | 0.50 |
| H4A | 0.6230 | 0.4514 | −0.4151 | 0.145 (19)* | 0.50 |
| H4B | 0.6104 | 0.4998 | −0.2885 | 0.133 (17)* | 0.50 |
| C5 | 0.4662 (7) | 0.5000 | −0.5000 | 0.079 (3) | 0.50 |
| H5B | 0.4055 | 0.5252 | −0.4409 | 0.118* | 0.25 |
| H5C | 0.4055 | 0.4748 | −0.5591 | 0.118* | 0.25 |
| C7 | 0.6267 (2) | 0.29466 (8) | 0.5523 (2) | 0.0798 (6) | |
| H7A | 0.7111 | 0.2946 | 0.4751 | 0.114 (7)* | |
| H7B | 0.6293 | 0.3252 | 0.6289 | 0.109 (6)* | |
| C8 | 0.5000 | 0.2500 | 0.7842 (4) | 0.0732 (10) | |
| H8A | 0.5000 | 0.2800 | 0.8635 | 0.11 (6)* | 0.50 |
| H8B | 0.5000 | 0.2200 | 0.8635 | 0.11 (6)* | 0.50 |
| C9 | 0.5000 | 0.2500 | 0.3177 (4) | 0.0569 (7) | |
| H9A | 0.5833 | 0.2500 | 0.2385 | 0.06 (3)* | 0.50 |
| H9B | 0.4167 | 0.2500 | 0.2385 | 0.08 (4)* | 0.50 |
Atomic displacement parameters (Å2) top| | U11 | U22 | U33 | U12 | U13 | U23 |
| O1 | 0.100 (2) | 0.1015 (18) | 0.0958 (18) | −0.0275 (16) | −0.0252 (17) | 0.0294 (16) |
| O2A | 0.074 (5) | 0.232 (11) | 0.111 (7) | −0.083 (6) | 0.003 (5) | 0.047 (7) |
| O2B | 0.109 (6) | 0.108 (4) | 0.082 (4) | −0.065 (4) | −0.019 (4) | 0.033 (3) |
| N1 | 0.0748 (13) | 0.0618 (10) | 0.0546 (9) | 0.000 | 0.000 | 0.0048 (8) |
| N2 | 0.0462 (11) | 0.1139 (15) | 0.0517 (9) | 0.000 | −0.0103 (8) | 0.000 |
| C1 | 0.086 (2) | 0.0550 (13) | 0.0741 (15) | 0.000 | 0.000 | 0.0046 (11) |
| C2 | 0.077 (2) | 0.0646 (17) | 0.0776 (19) | −0.0102 (16) | −0.0014 (16) | 0.0102 (17) |
| C3 | 0.081 (7) | 0.0614 (14) | 0.0837 (16) | −0.005 (2) | −0.001 (2) | 0.0100 (13) |
| C4 | 0.093 (3) | 0.082 (2) | 0.085 (2) | −0.0042 (18) | 0.0022 (18) | 0.028 (2) |
| C5 | 0.083 (8) | 0.066 (2) | 0.089 (3) | 0.000 | 0.000 | 0.012 (2) |
| C7 | 0.0700 (12) | 0.1003 (12) | 0.0691 (10) | −0.0321 (9) | −0.0016 (9) | −0.0086 (9) |
| C8 | 0.068 (2) | 0.109 (3) | 0.0422 (14) | 0.000 | 0.000 | 0.000 |
| C9 | 0.0495 (17) | 0.0789 (19) | 0.0424 (12) | 0.000 | 0.000 | 0.000 |
Geometric parameters (Å, º) top
| O1—O2Ai | 0.914 (9) | C1—C2i | 1.529 (4) |
| O1—C1 | 1.367 (3) | C1—C2 | 1.529 (4) |
| O1—O2Bi | 1.493 (8) | C2—C3 | 1.516 (7) |
| O1—O1i | 1.720 (7) | C2—H2A | 0.9700 |
| O1—H1 | 1.34 (4) | C2—H2B | 0.9700 |
| O2A—O2B | 0.735 (13) | C3—C4 | 1.510 (6) |
| O2A—O1i | 0.914 (9) | C3—H3A | 0.9700 |
| O2A—C1 | 1.131 (9) | C3—H3B | 0.9700 |
| O2A—C2i | 1.748 (11) | C4—C5 | 1.518 (5) |
| O2A—H7Bii | 2.7267 | C4—H4A | 0.9700 |
| O2B—C1 | 1.100 (8) | C4—H4B | 0.9700 |
| O2B—O2Bi | 1.447 (18) | C5—C4iv | 1.518 (5) |
| O2B—O1i | 1.493 (8) | C5—H5B | 0.9700 |
| O2B—C2i | 1.790 (8) | C5—H5C | 0.9700 |
| N1—C9 | 1.467 (2) | C7—H7A | 0.9700 |
| N1—C7 | 1.473 (2) | C7—H7B | 0.9700 |
| N1—C7i | 1.473 (2) | C8—N2v | 1.460 (2) |
| N2—C7iii | 1.446 (2) | C8—H8A | 0.9700 |
| N2—C7 | 1.446 (2) | C8—H8B | 0.9700 |
| N2—C8 | 1.460 (2) | C9—N1iii | 1.467 (2) |
| C1—O2Bi | 1.100 (8) | C9—H9A | 0.9700 |
| C1—O2Ai | 1.131 (9) | C9—H9B | 0.9700 |
| C1—O1i | 1.367 (3) | | |
| | | |
| O2Ai—O1—C1 | 55.2 (6) | O2A—C1—C2i | 80.7 (6) |
| O2Ai—O1—O2Bi | 22.4 (9) | O2Ai—C1—C2i | 135.1 (6) |
| C1—O1—O2Bi | 45.0 (3) | O1—C1—C2i | 152.2 (3) |
| O2Ai—O1—O1i | 103.0 (6) | O1i—C1—C2i | 107.69 (19) |
| C1—O1—O1i | 51.04 (16) | O2B—C1—C2 | 120.4 (4) |
| O2Bi—O1—O1i | 84.8 (4) | O2Bi—C1—C2 | 84.2 (5) |
| O2Ai—O1—H1 | 121 (2) | O2A—C1—C2 | 135.1 (6) |
| C1—O1—H1 | 93.0 (19) | O2Ai—C1—C2 | 80.7 (6) |
| O2Bi—O1—H1 | 99 (2) | O1—C1—C2 | 107.69 (19) |
| O1i—O1—H1 | 50.2 (16) | O1i—C1—C2 | 152.2 (3) |
| O2B—O2A—O1i | 129.4 (19) | C2i—C1—C2 | 55.0 (3) |
| O2B—O2A—C1 | 68.5 (11) | C3—C2—C1 | 112.8 (4) |
| O1i—O2A—C1 | 83.2 (8) | C3—C2—H2A | 109.0 |
| O2B—O2A—C2i | 81.2 (12) | C1—C2—H2A | 109.0 |
| O1i—O2A—C2i | 119.7 (11) | C3—C2—H2B | 109.0 |
| C1—O2A—C2i | 59.6 (5) | C1—C2—H2B | 109.0 |
| O2B—O2A—H7Bii | 104.3 | H2A—C2—H2B | 107.8 |
| O1i—O2A—H7Bii | 98.7 | C4—C3—C2 | 111.7 (7) |
| C1—O2A—H7Bii | 171.3 | C4—C3—H3A | 109.3 |
| C2i—O2A—H7Bii | 125.3 | C2—C3—H3A | 109.3 |
| O2A—O2B—C1 | 73.1 (12) | C4—C3—H3B | 109.3 |
| O2A—O2B—O2Bi | 117.8 (13) | C2—C3—H3B | 109.3 |
| C1—O2B—O2Bi | 48.9 (5) | H3A—C3—H3B | 107.9 |
| O2A—O2B—O1i | 28.3 (11) | C3—C4—C5 | 116.2 (5) |
| C1—O2B—O1i | 61.5 (4) | C3—C4—H4A | 108.2 |
| O2Bi—O2B—O1i | 95.2 (4) | C5—C4—H4A | 108.2 |
| O2A—O2B—C2i | 74.9 (13) | C3—C4—H4B | 108.2 |
| C1—O2B—C2i | 58.2 (4) | C5—C4—H4B | 108.2 |
| O2Bi—O2B—C2i | 89.4 (3) | H4A—C4—H4B | 107.4 |
| O1i—O2B—C2i | 90.5 (5) | C4—C5—C4iv | 112.3 (5) |
| C9—N1—C7 | 107.79 (12) | C4—C5—H5B | 109.1 |
| C9—N1—C7i | 107.79 (12) | C4iv—C5—H5B | 109.1 |
| C7—N1—C7i | 108.26 (18) | C4—C5—H5C | 109.1 |
| C7iii—N2—C7 | 107.62 (18) | C4iv—C5—H5C | 109.1 |
| C7iii—N2—C8 | 108.71 (12) | H5B—C5—H5C | 107.9 |
| C7—N2—C8 | 108.71 (12) | N2—C7—N1 | 112.28 (14) |
| O2B—C1—O2Bi | 82.3 (10) | N2—C7—H7A | 109.1 |
| O2B—C1—O2A | 38.4 (7) | N1—C7—H7A | 109.1 |
| O2Bi—C1—O2A | 117.2 (8) | N2—C7—H7B | 109.1 |
| O2B—C1—O2Ai | 117.2 (8) | N1—C7—H7B | 109.1 |
| O2Bi—C1—O2Ai | 38.4 (7) | H7A—C7—H7B | 107.9 |
| O2A—C1—O2Ai | 140.9 (13) | N2—C8—N2v | 112.0 (2) |
| O2B—C1—O1 | 123.0 (5) | N2—C8—H8A | 109.2 |
| O2Bi—C1—O1 | 73.6 (4) | N2v—C8—H8A | 109.2 |
| O2A—C1—O1 | 115.9 (6) | N2—C8—H8B | 109.2 |
| O2Ai—C1—O1 | 41.6 (5) | N2v—C8—H8B | 109.2 |
| O2B—C1—O1i | 73.6 (4) | H8A—C8—H8B | 107.9 |
| O2Bi—C1—O1i | 123.0 (5) | N1—C9—N1iii | 111.3 (2) |
| O2A—C1—O1i | 41.6 (5) | N1—C9—H9A | 109.4 |
| O2Ai—C1—O1i | 115.9 (6) | N1iii—C9—H9A | 109.4 |
| O1—C1—O1i | 77.9 (3) | N1—C9—H9B | 109.4 |
| O2B—C1—C2i | 84.2 (5) | N1iii—C9—H9B | 109.4 |
| O2Bi—C1—C2i | 120.4 (4) | H9A—C9—H9B | 108.0 |
| | | |
| O1i—O2A—O2B—C1 | −60.7 (19) | O1i—O2A—C1—O1 | 26.1 (12) |
| C2i—O2A—O2B—C1 | 60.7 (3) | C2i—O2A—C1—O1 | 156.5 (4) |
| H7Bii—O2A—O2B—C1 | −174.9 | H7Bii—O2A—C1—O1 | −76.7 |
| O1i—O2A—O2B—O2Bi | −40 (3) | O2B—O2A—C1—O1i | −137.3 (19) |
| C1—O2A—O2B—O2Bi | 20.4 (8) | C2i—O2A—C1—O1i | 130.4 (9) |
| C2i—O2A—O2B—O2Bi | 81.1 (8) | H7Bii—O2A—C1—O1i | −102.8 |
| H7Bii—O2A—O2B—O2Bi | −154.5 | O2B—O2A—C1—C2i | 92.3 (12) |
| C1—O2A—O2B—O1i | 60.7 (19) | O1i—O2A—C1—C2i | −130.4 (9) |
| C2i—O2A—O2B—O1i | 121 (2) | H7Bii—O2A—C1—C2i | 126.8 |
| H7Bii—O2A—O2B—O1i | −114.2 | O2B—O2A—C1—C2 | 83.6 (16) |
| O1i—O2A—O2B—C2i | −121 (2) | O1i—O2A—C1—C2 | −139.2 (6) |
| C1—O2A—O2B—C2i | −60.7 (3) | C2i—O2A—C1—C2 | −8.8 (8) |
| H7Bii—O2A—O2B—C2i | 124.4 | H7Bii—O2A—C1—C2 | 118.1 |
| O2A—O2B—C1—O2Bi | 155.8 (11) | O2Ai—O1—C1—O2B | 95.1 (13) |
| O1i—O2B—C1—O2Bi | 127.8 (4) | O2Bi—O1—C1—O2B | 69.0 (10) |
| C2i—O2B—C1—O2Bi | −121.8 (4) | O1i—O1—C1—O2B | −61.1 (6) |
| O2Bi—O2B—C1—O2A | −155.8 (11) | O2Ai—O1—C1—O2Bi | 26.1 (13) |
| O1i—O2B—C1—O2A | −28.0 (12) | O1i—O1—C1—O2Bi | −130.1 (5) |
| C2i—O2B—C1—O2A | 82.4 (13) | O2Ai—O1—C1—O2A | 138.8 (18) |
| O2A—O2B—C1—O2Ai | 139.2 (17) | O2Bi—O1—C1—O2A | 112.7 (9) |
| O2Bi—O2B—C1—O2Ai | −16.6 (7) | O1i—O1—C1—O2A | −17.4 (8) |
| O1i—O2B—C1—O2Ai | 111.2 (7) | O2Bi—O1—C1—O2Ai | −26.1 (13) |
| C2i—O2B—C1—O2Ai | −138.4 (6) | O1i—O1—C1—O2Ai | −156.2 (11) |
| O2A—O2B—C1—O1 | 91.2 (14) | O2Ai—O1—C1—O1i | 156.2 (11) |
| O2Bi—O2B—C1—O1 | −64.7 (4) | O2Bi—O1—C1—O1i | 130.1 (5) |
| O1i—O2B—C1—O1 | 63.2 (5) | O2Ai—O1—C1—C2i | −98.8 (11) |
| C2i—O2B—C1—O1 | 173.5 (4) | O2Bi—O1—C1—C2i | −124.8 (7) |
| O2A—O2B—C1—O1i | 28.0 (12) | O1i—O1—C1—C2i | 105.1 (5) |
| O2Bi—O2B—C1—O1i | −127.8 (4) | O2Ai—O1—C1—C2 | −52.1 (11) |
| C2i—O2B—C1—O1i | 110.4 (3) | O2Bi—O1—C1—C2 | −78.2 (5) |
| O2A—O2B—C1—C2i | −82.4 (13) | O1i—O1—C1—C2 | 151.8 (3) |
| O2Bi—O2B—C1—C2i | 121.8 (4) | O2B—C1—C2—C3 | 41.6 (7) |
| O1i—O2B—C1—C2i | −110.4 (3) | O2Bi—C1—C2—C3 | 119.1 (5) |
| O2A—O2B—C1—C2 | −125.6 (12) | O2A—C1—C2—C3 | −4.1 (11) |
| O2Bi—O2B—C1—C2 | 78.6 (5) | O2Ai—C1—C2—C3 | 157.8 (7) |
| O1i—O2B—C1—C2 | −153.6 (3) | O1—C1—C2—C3 | −170.2 (3) |
| C2i—O2B—C1—C2 | −43.2 (4) | O1i—C1—C2—C3 | −72.5 (6) |
| O1i—O2A—C1—O2B | 137.3 (19) | C2i—C1—C2—C3 | −14.7 (3) |
| C2i—O2A—C1—O2B | −92.3 (12) | C1—C2—C3—C4 | −173.7 (3) |
| H7Bii—O2A—C1—O2B | 34.5 | C2—C3—C4—C5 | −175.7 (3) |
| O2B—O2A—C1—O2Bi | −27.1 (13) | C3—C4—C5—C4iv | −174.8 (4) |
| O1i—O2A—C1—O2Bi | 110.1 (11) | C7iii—N2—C7—N1 | 59.7 (2) |
| C2i—O2A—C1—O2Bi | −119.5 (5) | C8—N2—C7—N1 | −57.90 (19) |
| H7Bii—O2A—C1—O2Bi | 7.3 | C9—N1—C7—N2 | −59.39 (18) |
| O2B—O2A—C1—O2Ai | −67 (2) | C7i—N1—C7—N2 | 57.0 (2) |
| O1i—O2A—C1—O2Ai | 70 (2) | C7iii—N2—C8—N2v | −58.44 (10) |
| C2i—O2A—C1—O2Ai | −159.6 (16) | C7—N2—C8—N2v | 58.44 (10) |
| H7Bii—O2A—C1—O2Ai | −32.8 | C7—N1—C9—N1iii | 58.33 (11) |
| O2B—O2A—C1—O1 | −111.2 (11) | C7i—N1—C9—N1iii | −58.33 (11) |
| Symmetry codes: (i) −x+1, y, z; (ii) x−1/2, y, z−1/2; (iii) x, −y+1/2, z; (iv) x, −y+1, −z−1; (v) −x+1, −y+1/2, z. |
Hydrogen-bond geometry (Å, º) top
| D—H···A | D—H | H···A | D···A | D—H···A |
| O1—H1···N1 | 1.34 (4) | 1.56 (6) | 2.732 (3) | 140 (2) |
| C7—H7B···O2Avi | 0.97 | 2.73 | 3.185 (10) | 110 |
| C7—H7A···O2Bvi | 0.97 | 2.60 | 3.240 (8) | 124 |
| C8—H8B···O2Bvii | 0.97 | 2.41 | 3.348 (9) | 161 |
| C9—H9B···N2ii | 0.97 | 2.76 | 3.654 (2) | 154 |
| C2—H2B···O1viii | 0.97 | 2.78 | 3.730 (5) | 166 |
| Symmetry codes: (ii) x−1/2, y, z−1/2; (vi) x+1/2, y, z+1/2; (vii) x, −y+1/2, z+1; (viii) −x+3/2, y, z−1/2. |

 Subscribe to Acta Crystallographica Section B: Structural Science, Crystal Engineering and Materials
Subscribe to Acta Crystallographica Section B: Structural Science, Crystal Engineering and Materials
The full text of this article is available to subscribers to the journal.
If you have already registered and are using a computer listed in your registration details, please email
[email protected] for assistance.
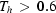 ). The system may be understood as an OD (order–disorder) structure based on a layer with layer group
). The system may be understood as an OD (order–disorder) structure based on a layer with layer group 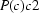 and cell
and cell 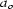 ≃ 4.7,
≃ 4.7, 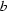 ≃ 26.1 and
≃ 26.1 and  ≃ 14.4 Å. At 338 K the layer stacking is random, but with decreasing temperature the build-up of an orthorhombic MDO (maximal degree of order) structure with cell a
≃ 14.4 Å. At 338 K the layer stacking is random, but with decreasing temperature the build-up of an orthorhombic MDO (maximal degree of order) structure with cell a = 2a
= 2a , b
, b = b, c
= b, c = c and space group
= c and space group 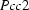 is begun (at ∼301 K). The superposition structure of the OD system at T = 286 (1) K with space group
is begun (at ∼301 K). The superposition structure of the OD system at T = 286 (1) K with space group 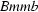 and cell
and cell 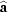 =
= 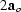 ,
, 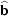 =
= 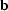 and
and 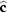 =
= 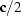 owes its cohesion to van der Waals interactions between the AA chains and to three types of hydrogen bonds of varied strength between U—U and U—AA. Before reaching completion, this MDO structure is transformed, at 282 K, into a monoclinic one with cell a
owes its cohesion to van der Waals interactions between the AA chains and to three types of hydrogen bonds of varied strength between U—U and U—AA. Before reaching completion, this MDO structure is transformed, at 282 K, into a monoclinic one with cell a = −a
= −a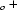 c/4, b
c/4, b = b, c
= b, c = −2
= −2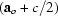 , space group
, space group 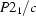 , spontaneous deformation ∼2°, and ferroelastic domains. This transformation is achieved in two steps: first a furtive triggering transition, which is not yet fully understood, and second an improper ferroelastic transition. At ∼233 K, the system reaches its ground state (cell
, spontaneous deformation ∼2°, and ferroelastic domains. This transformation is achieved in two steps: first a furtive triggering transition, which is not yet fully understood, and second an improper ferroelastic transition. At ∼233 K, the system reaches its ground state (cell 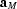 =
= 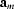 ,
, 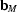 =
= 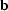 ,
, 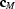 =
= 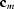 and space group
and space group 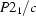 ) via an irreversible transition. The phase transitions below 338 K are described by a model based on the interaction of two thermally activated slip systems. The OD structure is described in terms of a three-dimensional Monte Carlo model that involves first- and second-neighbour interactions along the a axis and first-neighbour interactions along the b and c axes. This model includes random shifts of the chains along their axes and satisfactorily accounts for most features that are seen in the observed diffraction pattern.
) via an irreversible transition. The phase transitions below 338 K are described by a model based on the interaction of two thermally activated slip systems. The OD structure is described in terms of a three-dimensional Monte Carlo model that involves first- and second-neighbour interactions along the a axis and first-neighbour interactions along the b and c axes. This model includes random shifts of the chains along their axes and satisfactorily accounts for most features that are seen in the observed diffraction pattern.
 journal menu
journal menu









 Subscribe to Acta Crystallographica Section B: Structural Science, Crystal Engineering and Materials
Subscribe to Acta Crystallographica Section B: Structural Science, Crystal Engineering and Materials


