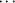 O = 2.620 (2) Å and O—H
O = 2.620 (2) Å and O—H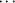 O = 163 (3)°] in which all carboxyl groups adopt the rare anti conformation, while the ketone group does not participate in the hydrogen bonding. The occurrence and energetics of this conformation are discussed. One intermolecular C—H
O = 163 (3)°] in which all carboxyl groups adopt the rare anti conformation, while the ketone group does not participate in the hydrogen bonding. The occurrence and energetics of this conformation are discussed. One intermolecular C—H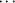 O close contact exists, which plays a role in stabilizing the hydrogen-bonding arrangement.
O close contact exists, which plays a role in stabilizing the hydrogen-bonding arrangement.Supporting information
Crystallographic Information File (CIF) https://doi.org/10.1107/S0108270107047014/ga3075sup1.cif | |
Structure factor file (CIF format) https://doi.org/10.1107/S0108270107047014/ga3075Isup2.hkl |
CCDC reference: 669187
(+)-3-Hydroxy-5β-Δ11-24-norcholenic acid, of known rotation and absolute configuration (Fieser & Fieser, 1959), was purchased from Steraloids Inc., Newport, Rhode Island, USA, and converted to (I) by catalytic hydrogenation of the C11═C12 double bond, followed by Jones oxidation (Bowden et al., 1946; Bladon et al., 1951; Bowers et al., 1953; Djerassi et al., 1956) to the ketone. Crystals of (I) were obtained from acetic acid (m.p. 457 K). The KBr IR spectrum of (I) displays a single absorption for both C═O groups at 1711 cm−1, essentially unchanged at 1706 cm−1 in CHCl3 solution, where dimers predominate.
All H atoms were found in electron density difference maps. The O-bound H atom was allowed to refine fully. The methyl H atoms were placed in ideally staggered positions with C—H distances of 0.98 Å [Uiso(H) = 1.5Ueq(C)]. The methylene and methine H atoms were placed in geometrically idealized positions and constrained to ride on their parent C atoms with C—H distances of 0.99 and 1.00 Å, respectively [Uiso(H) = 1.2Ueq(C)].
Data collection: APEX2 (Bruker, 2006); cell refinement: APEX2 (Bruker, 2006); data reduction: SAINT (Bruker, 2005); program(s) used to solve structure: SHELXTL (Sheldrick, 2004); program(s) used to refine structure: SHELXTL (Sheldrick, 2004); molecular graphics: SHELXTL (Sheldrick, 2004); software used to prepare material for publication: SHELXTL (Sheldrick, 2004).
| C23H36O3 | Dx = 1.215 Mg m−3 |
| Mr = 360.52 | Melting point: 457 K |
| Orthorhombic, P212121 | Cu Kα radiation, λ = 1.54178 Å |
| Hall symbol: P 2ac 2ab | Cell parameters from 13991 reflections |
| a = 7.47160 (11) Å | θ = 5.3–68.1° |
| b = 8.72260 (12) Å | µ = 0.61 mm−1 |
| c = 30.2407 (5) Å | T = 100 K |
| V = 1970.84 (5) Å3 | Needle, colourless |
| Z = 4 | 0.31 × 0.04 × 0.04 mm |
| F(000) = 792 |
| Bruker SMART CCD APEXII area-detector diffractometer | 3567 independent reflections |
| Radiation source: fine-focus sealed tube | 2976 reflections with I > 2σ(I) |
| Graphite monochromator | Rint = 0.062 |
| ϕ and ω scans | θmax = 68.1°, θmin = 5.3° |
| Absorption correction: multi-scan (SADABS; Sheldrick, 2001) | h = −8→8 |
| Tmin = 0.834, Tmax = 0.976 | k = −8→10 |
| 13991 measured reflections | l = −36→36 |
| Refinement on F2 | Hydrogen site location: inferred from neighbouring sites |
| Least-squares matrix: full | H atoms treated by a mixture of independent and constrained refinement |
| R[F2 > 2σ(F2)] = 0.040 | w = 1/[σ2(Fo2) + (0.0566P)2 + 0.0124P] where P = (Fo2 + 2Fc2)/3 |
| wR(F2) = 0.101 | (Δ/σ)max < 0.001 |
| S = 1.04 | Δρmax = 0.23 e Å−3 |
| 3567 reflections | Δρmin = −0.16 e Å−3 |
| 243 parameters | Extinction correction: SHELXTL (Sheldrick, 2004), Fc*=kFc[1+0.001xFc2λ3/sin(2θ)]-1/4 |
| 0 restraints | Extinction coefficient: 0.0015 (3) |
| Primary atom site location: structure-invariant direct methods | Absolute structure: Flack (1983), 1475 Friedel pairs |
| Secondary atom site location: difference Fourier map | Absolute structure parameter: 0.0 (2) |
| C23H36O3 | V = 1970.84 (5) Å3 |
| Mr = 360.52 | Z = 4 |
| Orthorhombic, P212121 | Cu Kα radiation |
| a = 7.47160 (11) Å | µ = 0.61 mm−1 |
| b = 8.72260 (12) Å | T = 100 K |
| c = 30.2407 (5) Å | 0.31 × 0.04 × 0.04 mm |
| Bruker SMART CCD APEXII area-detector diffractometer | 3567 independent reflections |
| Absorption correction: multi-scan (SADABS; Sheldrick, 2001) | 2976 reflections with I > 2σ(I) |
| Tmin = 0.834, Tmax = 0.976 | Rint = 0.062 |
| 13991 measured reflections |
| R[F2 > 2σ(F2)] = 0.040 | H atoms treated by a mixture of independent and constrained refinement |
| wR(F2) = 0.101 | Δρmax = 0.23 e Å−3 |
| S = 1.04 | Δρmin = −0.16 e Å−3 |
| 3567 reflections | Absolute structure: Flack (1983), 1475 Friedel pairs |
| 243 parameters | Absolute structure parameter: 0.0 (2) |
| 0 restraints |
Experimental. crystal mounted on cryoloop using Paratone-N |
Geometry. All e.s.d.'s (except the e.s.d. in the dihedral angle between two l.s. planes) are estimated using the full covariance matrix. The cell e.s.d.'s are taken into account individually in the estimation of e.s.d.'s in distances, angles and torsion angles; correlations between e.s.d.'s in cell parameters are only used when they are defined by crystal symmetry. An approximate (isotropic) treatment of cell e.s.d.'s is used for estimating e.s.d.'s involving l.s. planes. |
Refinement. Refinement of F2 against ALL reflections. The weighted R-factor wR and goodness of fit S are based on F2, conventional R-factors R are based on F, with F set to zero for negative F2. The threshold expression of F2 > σ(F2) is used only for calculating R-factors(gt) etc. and is not relevant to the choice of reflections for refinement. R-factors based on F2 are statistically about twice as large as those based on F, and R- factors based on ALL data will be even larger. |
| x | y | z | Uiso*/Ueq | ||
| O1 | 0.6083 (3) | −0.15613 (19) | 0.71061 (5) | 0.0511 (5) | |
| C1 | 0.2064 (3) | −0.1941 (2) | 0.76545 (6) | 0.0313 (5) | |
| H1A | 0.2247 | −0.3012 | 0.7556 | 0.038* | |
| H1B | 0.0777 | −0.1699 | 0.7619 | 0.038* | |
| O2 | −0.4200 (2) | 0.60243 (15) | 0.98058 (5) | 0.0306 (4) | |
| C2 | 0.3151 (3) | −0.0876 (2) | 0.73540 (6) | 0.0333 (5) | |
| H2A | 0.2799 | −0.1034 | 0.7042 | 0.040* | |
| H2B | 0.2912 | 0.0207 | 0.7432 | 0.040* | |
| O3 | −0.2355 (2) | 0.78290 (16) | 1.00117 (5) | 0.0372 (4) | |
| H3 | −0.113 (4) | 0.811 (3) | 1.0039 (9) | 0.066 (9)* | |
| C3 | 0.5105 (3) | −0.1221 (2) | 0.74108 (7) | 0.0349 (6) | |
| C4 | 0.5744 (3) | −0.1164 (2) | 0.78827 (7) | 0.0331 (5) | |
| H4A | 0.5737 | −0.0086 | 0.7985 | 0.040* | |
| H4B | 0.6993 | −0.1538 | 0.7896 | 0.040* | |
| C5 | 0.4579 (3) | −0.2135 (2) | 0.81969 (6) | 0.0283 (5) | |
| H5 | 0.4779 | −0.3234 | 0.8117 | 0.034* | |
| C6 | 0.5219 (3) | −0.1934 (2) | 0.86770 (7) | 0.0321 (5) | |
| H6A | 0.4666 | −0.2736 | 0.8864 | 0.038* | |
| H6B | 0.6534 | −0.2072 | 0.8689 | 0.038* | |
| C7 | 0.4741 (3) | −0.0358 (2) | 0.88631 (6) | 0.0272 (5) | |
| H7A | 0.5102 | −0.0307 | 0.9178 | 0.033* | |
| H7B | 0.5414 | 0.0440 | 0.8700 | 0.033* | |
| C8 | 0.2742 (3) | −0.00339 (19) | 0.88256 (6) | 0.0231 (4) | |
| H8 | 0.2081 | −0.0786 | 0.9014 | 0.028* | |
| C9 | 0.2100 (3) | −0.02122 (19) | 0.83429 (6) | 0.0231 (4) | |
| H9 | 0.2809 | 0.0542 | 0.8166 | 0.028* | |
| C10 | 0.2553 (3) | −0.1823 (2) | 0.81482 (6) | 0.0255 (5) | |
| C11 | 0.0154 (3) | 0.0250 (2) | 0.82891 (6) | 0.0296 (5) | |
| H11A | −0.0607 | −0.0536 | 0.8432 | 0.035* | |
| H11B | −0.0142 | 0.0256 | 0.7970 | 0.035* | |
| C12 | −0.0315 (3) | 0.1824 (2) | 0.84848 (6) | 0.0249 (4) | |
| H12A | −0.1623 | 0.1990 | 0.8464 | 0.030* | |
| H12B | 0.0286 | 0.2636 | 0.8311 | 0.030* | |
| C13 | 0.0272 (3) | 0.1943 (2) | 0.89724 (6) | 0.0220 (4) | |
| C14 | 0.2283 (3) | 0.1588 (2) | 0.89821 (6) | 0.0229 (4) | |
| H14 | 0.2869 | 0.2313 | 0.8771 | 0.028* | |
| C15 | 0.2882 (3) | 0.2058 (2) | 0.94461 (6) | 0.0261 (5) | |
| H15A | 0.4164 | 0.2345 | 0.9449 | 0.031* | |
| H15B | 0.2684 | 0.1218 | 0.9661 | 0.031* | |
| C16 | 0.1688 (3) | 0.3450 (2) | 0.95528 (6) | 0.0274 (5) | |
| H16A | 0.2419 | 0.4395 | 0.9568 | 0.033* | |
| H16B | 0.1086 | 0.3303 | 0.9841 | 0.033* | |
| C17 | 0.0279 (3) | 0.3582 (2) | 0.91774 (6) | 0.0239 (4) | |
| H17 | 0.0776 | 0.4296 | 0.8950 | 0.029* | |
| C18 | −0.0837 (3) | 0.0863 (2) | 0.92663 (6) | 0.0249 (5) | |
| H18A | −0.0719 | −0.0191 | 0.9158 | 0.037* | |
| H18B | −0.2098 | 0.1171 | 0.9257 | 0.037* | |
| H18C | −0.0400 | 0.0922 | 0.9571 | 0.037* | |
| C19 | 0.1503 (3) | −0.3099 (2) | 0.83858 (7) | 0.0331 (5) | |
| H19A | 0.0220 | −0.2968 | 0.8329 | 0.050* | |
| H19B | 0.1728 | −0.3039 | 0.8705 | 0.050* | |
| H19C | 0.1891 | −0.4100 | 0.8275 | 0.050* | |
| C20 | −0.1516 (3) | 0.4259 (2) | 0.93356 (6) | 0.0237 (4) | |
| H20 | −0.2007 | 0.3573 | 0.9571 | 0.028* | |
| C21 | −0.2902 (3) | 0.4377 (2) | 0.89678 (6) | 0.0294 (5) | |
| H21A | −0.2388 | 0.4934 | 0.8717 | 0.044* | |
| H21B | −0.3956 | 0.4928 | 0.9077 | 0.044* | |
| H21C | −0.3253 | 0.3345 | 0.8873 | 0.044* | |
| C22 | −0.1164 (3) | 0.5847 (2) | 0.95421 (7) | 0.0288 (5) | |
| H22A | −0.0129 | 0.5757 | 0.9745 | 0.035* | |
| H22B | −0.0816 | 0.6561 | 0.9302 | 0.035* | |
| C23 | −0.2696 (3) | 0.6550 (2) | 0.97937 (6) | 0.0262 (5) |
| U11 | U22 | U33 | U12 | U13 | U23 | |
| O1 | 0.0603 (13) | 0.0533 (10) | 0.0397 (9) | 0.0030 (10) | 0.0220 (9) | −0.0065 (8) |
| C1 | 0.0340 (13) | 0.0276 (9) | 0.0323 (10) | −0.0017 (10) | 0.0033 (10) | −0.0096 (8) |
| O2 | 0.0288 (9) | 0.0256 (7) | 0.0375 (7) | −0.0022 (7) | 0.0027 (7) | −0.0041 (6) |
| C2 | 0.0480 (15) | 0.0305 (10) | 0.0213 (9) | −0.0030 (10) | 0.0018 (10) | −0.0056 (8) |
| O3 | 0.0308 (10) | 0.0302 (7) | 0.0506 (9) | −0.0009 (7) | 0.0031 (8) | −0.0168 (7) |
| C3 | 0.0446 (15) | 0.0235 (9) | 0.0367 (12) | −0.0067 (10) | 0.0114 (11) | −0.0036 (8) |
| C4 | 0.0261 (13) | 0.0315 (11) | 0.0415 (11) | −0.0024 (10) | 0.0079 (10) | −0.0058 (9) |
| C5 | 0.0315 (13) | 0.0204 (9) | 0.0329 (10) | 0.0031 (9) | 0.0056 (9) | −0.0024 (8) |
| C6 | 0.0290 (13) | 0.0278 (10) | 0.0394 (11) | 0.0072 (10) | 0.0006 (10) | 0.0030 (8) |
| C7 | 0.0279 (12) | 0.0264 (9) | 0.0274 (10) | 0.0019 (9) | −0.0016 (9) | −0.0013 (7) |
| C8 | 0.0255 (12) | 0.0197 (8) | 0.0241 (9) | 0.0015 (8) | 0.0014 (8) | 0.0012 (7) |
| C9 | 0.0262 (12) | 0.0188 (8) | 0.0242 (9) | −0.0010 (8) | 0.0015 (9) | 0.0002 (7) |
| C10 | 0.0289 (12) | 0.0194 (8) | 0.0283 (9) | −0.0013 (9) | 0.0046 (9) | −0.0033 (7) |
| C11 | 0.0364 (14) | 0.0275 (10) | 0.0247 (9) | 0.0061 (9) | −0.0063 (10) | −0.0051 (7) |
| C12 | 0.0276 (12) | 0.0216 (9) | 0.0256 (9) | 0.0024 (9) | −0.0040 (9) | 0.0001 (7) |
| C13 | 0.0247 (11) | 0.0190 (8) | 0.0222 (9) | 0.0001 (8) | 0.0005 (9) | −0.0017 (7) |
| C14 | 0.0266 (12) | 0.0217 (8) | 0.0205 (8) | −0.0019 (9) | 0.0000 (9) | 0.0005 (7) |
| C15 | 0.0267 (12) | 0.0275 (9) | 0.0241 (9) | −0.0029 (9) | −0.0018 (9) | −0.0018 (7) |
| C16 | 0.0256 (12) | 0.0293 (10) | 0.0274 (9) | −0.0014 (9) | 0.0007 (9) | −0.0058 (8) |
| C17 | 0.0286 (12) | 0.0214 (9) | 0.0216 (8) | −0.0029 (9) | 0.0011 (9) | −0.0010 (7) |
| C18 | 0.0238 (12) | 0.0231 (9) | 0.0279 (9) | 0.0017 (9) | −0.0010 (9) | −0.0008 (7) |
| C19 | 0.0364 (14) | 0.0205 (9) | 0.0425 (12) | −0.0012 (9) | 0.0094 (10) | −0.0017 (8) |
| C20 | 0.0267 (12) | 0.0204 (9) | 0.0240 (9) | 0.0011 (9) | 0.0017 (9) | −0.0021 (7) |
| C21 | 0.0344 (13) | 0.0259 (9) | 0.0278 (9) | 0.0067 (9) | −0.0004 (10) | −0.0032 (8) |
| C22 | 0.0317 (13) | 0.0252 (10) | 0.0294 (9) | −0.0008 (9) | 0.0035 (10) | −0.0034 (8) |
| C23 | 0.0316 (13) | 0.0184 (8) | 0.0288 (9) | 0.0004 (9) | 0.0007 (9) | −0.0003 (7) |
| O1—C3 | 1.213 (3) | C11—H11B | 0.9900 |
| C1—C2 | 1.533 (3) | C12—C13 | 1.542 (2) |
| C1—C10 | 1.541 (3) | C12—H12A | 0.9900 |
| C1—H1A | 0.9900 | C12—H12B | 0.9900 |
| C1—H1B | 0.9900 | C13—C14 | 1.535 (3) |
| O2—C23 | 1.215 (3) | C13—C18 | 1.537 (3) |
| C2—C3 | 1.500 (4) | C13—C17 | 1.558 (2) |
| C2—H2A | 0.9900 | C14—C15 | 1.529 (2) |
| C2—H2B | 0.9900 | C14—H14 | 1.0000 |
| O3—C23 | 1.320 (2) | C15—C16 | 1.541 (3) |
| O3—H3 | 0.95 (3) | C15—H15A | 0.9900 |
| C3—C4 | 1.506 (3) | C15—H15B | 0.9900 |
| C4—C5 | 1.542 (3) | C16—C17 | 1.553 (3) |
| C4—H4A | 0.9900 | C16—H16A | 0.9900 |
| C4—H4B | 0.9900 | C16—H16B | 0.9900 |
| C5—C6 | 1.539 (3) | C17—C20 | 1.541 (3) |
| C5—C10 | 1.545 (3) | C17—H17 | 1.0000 |
| C5—H5 | 1.0000 | C18—H18A | 0.9800 |
| C6—C7 | 1.528 (3) | C18—H18B | 0.9800 |
| C6—H6A | 0.9900 | C18—H18C | 0.9800 |
| C6—H6B | 0.9900 | C19—H19A | 0.9800 |
| C7—C8 | 1.524 (3) | C19—H19B | 0.9800 |
| C7—H7A | 0.9900 | C19—H19C | 0.9800 |
| C7—H7B | 0.9900 | C20—C21 | 1.523 (3) |
| C8—C14 | 1.530 (2) | C20—C22 | 1.542 (3) |
| C8—C9 | 1.544 (2) | C20—H20 | 1.0000 |
| C8—H8 | 1.0000 | C21—H21A | 0.9800 |
| C9—C11 | 1.518 (3) | C21—H21B | 0.9800 |
| C9—C10 | 1.560 (2) | C21—H21C | 0.9800 |
| C9—H9 | 1.0000 | C22—C23 | 1.505 (3) |
| C10—C19 | 1.540 (3) | C22—H22A | 0.9900 |
| C11—C12 | 1.535 (3) | C22—H22B | 0.9900 |
| C11—H11A | 0.9900 | ||
| C2—C1—C10 | 114.09 (17) | C11—C12—H12B | 109.4 |
| C2—C1—H1A | 108.7 | C13—C12—H12B | 109.4 |
| C10—C1—H1A | 108.7 | H12A—C12—H12B | 108.0 |
| C2—C1—H1B | 108.7 | C14—C13—C18 | 113.14 (16) |
| C10—C1—H1B | 108.7 | C14—C13—C12 | 106.44 (15) |
| H1A—C1—H1B | 107.6 | C18—C13—C12 | 111.01 (15) |
| C3—C2—C1 | 109.05 (18) | C14—C13—C17 | 100.03 (15) |
| C3—C2—H2A | 109.9 | C18—C13—C17 | 109.51 (15) |
| C1—C2—H2A | 109.9 | C12—C13—C17 | 116.30 (15) |
| C3—C2—H2B | 109.9 | C15—C14—C8 | 117.80 (15) |
| C1—C2—H2B | 109.9 | C15—C14—C13 | 104.48 (15) |
| H2A—C2—H2B | 108.3 | C8—C14—C13 | 113.56 (16) |
| C23—O3—H3 | 116.3 (17) | C15—C14—H14 | 106.8 |
| O1—C3—C2 | 123.3 (2) | C8—C14—H14 | 106.8 |
| O1—C3—C4 | 122.5 (2) | C13—C14—H14 | 106.8 |
| C2—C3—C4 | 114.23 (17) | C14—C15—C16 | 103.55 (15) |
| C3—C4—C5 | 112.79 (18) | C14—C15—H15A | 111.1 |
| C3—C4—H4A | 109.0 | C16—C15—H15A | 111.1 |
| C5—C4—H4A | 109.0 | C14—C15—H15B | 111.1 |
| C3—C4—H4B | 109.0 | C16—C15—H15B | 111.1 |
| C5—C4—H4B | 109.0 | H15A—C15—H15B | 109.0 |
| H4A—C4—H4B | 107.8 | C15—C16—C17 | 107.34 (15) |
| C6—C5—C4 | 110.10 (18) | C15—C16—H16A | 110.2 |
| C6—C5—C10 | 111.99 (17) | C17—C16—H16A | 110.2 |
| C4—C5—C10 | 113.39 (17) | C15—C16—H16B | 110.2 |
| C6—C5—H5 | 107.0 | C17—C16—H16B | 110.2 |
| C4—C5—H5 | 107.0 | H16A—C16—H16B | 108.5 |
| C10—C5—H5 | 107.0 | C20—C17—C16 | 113.04 (15) |
| C7—C6—C5 | 112.17 (16) | C20—C17—C13 | 118.16 (17) |
| C7—C6—H6A | 109.2 | C16—C17—C13 | 102.99 (15) |
| C5—C6—H6A | 109.2 | C20—C17—H17 | 107.4 |
| C7—C6—H6B | 109.2 | C16—C17—H17 | 107.4 |
| C5—C6—H6B | 109.2 | C13—C17—H17 | 107.4 |
| H6A—C6—H6B | 107.9 | C13—C18—H18A | 109.5 |
| C8—C7—C6 | 111.63 (17) | C13—C18—H18B | 109.5 |
| C8—C7—H7A | 109.3 | H18A—C18—H18B | 109.5 |
| C6—C7—H7A | 109.3 | C13—C18—H18C | 109.5 |
| C8—C7—H7B | 109.3 | H18A—C18—H18C | 109.5 |
| C6—C7—H7B | 109.3 | H18B—C18—H18C | 109.5 |
| H7A—C7—H7B | 108.0 | C10—C19—H19A | 109.5 |
| C7—C8—C14 | 111.57 (16) | C10—C19—H19B | 109.5 |
| C7—C8—C9 | 110.85 (16) | H19A—C19—H19B | 109.5 |
| C14—C8—C9 | 108.42 (14) | C10—C19—H19C | 109.5 |
| C7—C8—H8 | 108.6 | H19A—C19—H19C | 109.5 |
| C14—C8—H8 | 108.6 | H19B—C19—H19C | 109.5 |
| C9—C8—H8 | 108.6 | C21—C20—C17 | 112.99 (16) |
| C11—C9—C8 | 111.85 (16) | C21—C20—C22 | 110.55 (16) |
| C11—C9—C10 | 113.97 (16) | C17—C20—C22 | 108.74 (17) |
| C8—C9—C10 | 112.34 (15) | C21—C20—H20 | 108.1 |
| C11—C9—H9 | 106.0 | C17—C20—H20 | 108.1 |
| C8—C9—H9 | 106.0 | C22—C20—H20 | 108.1 |
| C10—C9—H9 | 106.0 | C20—C21—H21A | 109.5 |
| C19—C10—C1 | 106.44 (16) | C20—C21—H21B | 109.5 |
| C19—C10—C5 | 109.10 (17) | H21A—C21—H21B | 109.5 |
| C1—C10—C5 | 108.25 (16) | C20—C21—H21C | 109.5 |
| C19—C10—C9 | 111.34 (15) | H21A—C21—H21C | 109.5 |
| C1—C10—C9 | 112.00 (16) | H21B—C21—H21C | 109.5 |
| C5—C10—C9 | 109.59 (16) | C23—C22—C20 | 116.16 (18) |
| C9—C11—C12 | 114.48 (17) | C23—C22—H22A | 108.2 |
| C9—C11—H11A | 108.6 | C20—C22—H22A | 108.2 |
| C12—C11—H11A | 108.6 | C23—C22—H22B | 108.2 |
| C9—C11—H11B | 108.6 | C20—C22—H22B | 108.2 |
| C12—C11—H11B | 108.6 | H22A—C22—H22B | 107.4 |
| H11A—C11—H11B | 107.6 | O2—C23—O3 | 118.8 (2) |
| C11—C12—C13 | 111.35 (15) | O2—C23—C22 | 124.41 (17) |
| C11—C12—H12A | 109.4 | O3—C23—C22 | 116.74 (19) |
| C13—C12—H12A | 109.4 | ||
| C10—C1—C2—C3 | 57.7 (2) | C9—C11—C12—C13 | −53.2 (2) |
| C1—C2—C3—O1 | 124.0 (2) | C11—C12—C13—C14 | 56.0 (2) |
| C1—C2—C3—C4 | −53.9 (2) | C11—C12—C13—C18 | −67.5 (2) |
| O1—C3—C4—C5 | −126.8 (2) | C11—C12—C13—C17 | 166.41 (17) |
| C2—C3—C4—C5 | 51.2 (2) | C7—C8—C14—C15 | −54.6 (2) |
| C3—C4—C5—C6 | −175.90 (17) | C9—C8—C14—C15 | −176.92 (17) |
| C3—C4—C5—C10 | −49.6 (2) | C7—C8—C14—C13 | −177.15 (15) |
| C4—C5—C6—C7 | 72.3 (2) | C9—C8—C14—C13 | 60.5 (2) |
| C10—C5—C6—C7 | −54.9 (2) | C18—C13—C14—C15 | −69.84 (18) |
| C5—C6—C7—C8 | 55.1 (2) | C12—C13—C14—C15 | 167.97 (14) |
| C6—C7—C8—C14 | −176.02 (15) | C17—C13—C14—C15 | 46.55 (17) |
| C6—C7—C8—C9 | −55.1 (2) | C18—C13—C14—C8 | 59.8 (2) |
| C7—C8—C9—C11 | −174.62 (16) | C12—C13—C14—C8 | −62.38 (19) |
| C14—C8—C9—C11 | −51.8 (2) | C17—C13—C14—C8 | 176.20 (14) |
| C7—C8—C9—C10 | 55.7 (2) | C8—C14—C15—C16 | −161.05 (17) |
| C14—C8—C9—C10 | 178.52 (17) | C13—C14—C15—C16 | −33.97 (19) |
| C2—C1—C10—C19 | −173.25 (17) | C14—C15—C16—C17 | 7.8 (2) |
| C2—C1—C10—C5 | −56.1 (2) | C15—C16—C17—C20 | 149.14 (16) |
| C2—C1—C10—C9 | 64.8 (2) | C15—C16—C17—C13 | 20.5 (2) |
| C6—C5—C10—C19 | −68.42 (19) | C14—C13—C17—C20 | −165.65 (16) |
| C4—C5—C10—C19 | 166.24 (16) | C18—C13—C17—C20 | −46.6 (2) |
| C6—C5—C10—C1 | 176.13 (15) | C12—C13—C17—C20 | 80.3 (2) |
| C4—C5—C10—C1 | 50.8 (2) | C14—C13—C17—C16 | −40.27 (18) |
| C6—C5—C10—C9 | 53.7 (2) | C18—C13—C17—C16 | 78.8 (2) |
| C4—C5—C10—C9 | −71.6 (2) | C12—C13—C17—C16 | −154.35 (17) |
| C11—C9—C10—C19 | −62.4 (2) | C16—C17—C20—C21 | −179.56 (16) |
| C8—C9—C10—C19 | 66.1 (2) | C13—C17—C20—C21 | −59.2 (2) |
| C11—C9—C10—C1 | 56.7 (2) | C16—C17—C20—C22 | 57.3 (2) |
| C8—C9—C10—C1 | −174.80 (18) | C13—C17—C20—C22 | 177.62 (15) |
| C11—C9—C10—C5 | 176.81 (16) | C21—C20—C22—C23 | 66.9 (2) |
| C8—C9—C10—C5 | −54.7 (2) | C17—C20—C22—C23 | −168.55 (16) |
| C8—C9—C11—C12 | 50.5 (2) | C20—C22—C23—O2 | −7.4 (3) |
| C10—C9—C11—C12 | 179.25 (15) | C20—C22—C23—O3 | 172.93 (17) |
| D—H···A | D—H | H···A | D···A | D—H···A |
| O3—H3···O2i | 0.95 (3) | 1.69 (3) | 2.620 (2) | 163 (3) |
| C22—H22A···O3i | 0.99 | 2.52 | 3.354 (3) | 142 |
| Symmetry code: (i) x+1/2, −y+3/2, −z+2. |
Experimental details
| Crystal data | |
| Chemical formula | C23H36O3 |
| Mr | 360.52 |
| Crystal system, space group | Orthorhombic, P212121 |
| Temperature (K) | 100 |
| a, b, c (Å) | 7.47160 (11), 8.72260 (12), 30.2407 (5) |
| V (Å3) | 1970.84 (5) |
| Z | 4 |
| Radiation type | Cu Kα |
| µ (mm−1) | 0.61 |
| Crystal size (mm) | 0.31 × 0.04 × 0.04 |
| Data collection | |
| Diffractometer | Bruker SMART CCD APEXII area-detector diffractometer |
| Absorption correction | Multi-scan (SADABS; Sheldrick, 2001) |
| Tmin, Tmax | 0.834, 0.976 |
| No. of measured, independent and observed [I > 2σ(I)] reflections | 13991, 3567, 2976 |
| Rint | 0.062 |
| (sin θ/λ)max (Å−1) | 0.602 |
| Refinement | |
| R[F2 > 2σ(F2)], wR(F2), S | 0.040, 0.101, 1.04 |
| No. of reflections | 3567 |
| No. of parameters | 243 |
| H-atom treatment | H atoms treated by a mixture of independent and constrained refinement |
| Δρmax, Δρmin (e Å−3) | 0.23, −0.16 |
| Absolute structure | Flack (1983), 1475 Friedel pairs |
| Absolute structure parameter | 0.0 (2) |
Computer programs: APEX2 (Bruker, 2006), SAINT (Bruker, 2005), SHELXTL (Sheldrick, 2004).
| O2—C23 | 1.215 (3) | O3—C23 | 1.320 (2) |
| O2—C23—C22 | 124.41 (17) | O3—C23—C22 | 116.74 (19) |
| D—H···A | D—H | H···A | D···A | D—H···A |
| O3—H3···O2i | 0.95 (3) | 1.69 (3) | 2.620 (2) | 163 (3) |
| C22—H22A···O3i | 0.99 | 2.52 | 3.354 (3) | 142 |
| Symmetry code: (i) x+1/2, −y+3/2, −z+2. |

 journal menu
journal menu








![[Figure 1]](http://journals.iucr.org/c/issues/2007/11/00/ga3075/ga3075fig1thm.gif)
![[Figure 2]](http://journals.iucr.org/c/issues/2007/11/00/ga3075/ga3075fig2thm.gif)




Our study of factors affecting the choice of hydrogen-bonding mode in ketocarboxylic acids frequently employs chiral non-racemates, whose absence of centrosymmetry favors the ordinarily less common hydrogen-bonding modes by discouraging formation of carboxyl dimers. Within this category, steroids are among the most readily available subject materials. We report here the structure of the title compound, (I), a 24-norcholanic acid.
Fig. 1 shows the title compound with its steroid numbering. The few significant conformational options all lie in the C17 side-chain. The substituents on the C17—C20 and C20—C21 bonds are optimally staggered, and the carboxyl group is turned so that its plane coincides approximately with the C20—C22 bond [O2—C23—C22—C20 = −7.4 (3)°]. The disordering of carboxyl C—O bond lengths and C—C—O angles often seen in dimers may also be possible in acid-to-acid catemers (see below) when their geometry permits the underlying averaging processes involved (Kuduva et al., 1999; Das & Desiraju, 2006). However, in (I), these distances and angles all lie within the normal range for highly ordered carboxyl groups (Table 1). What is unusual in (I) is the seldom encountered anti arrangement of H and C=O in the carboxyl group, sometimes also called the antiplanar, transoid or E conformation. This is normal in internally hydrogen-bonded carboxyls (Coté et al., 1996) but is exceedingly rare in acid-to-acid catemers (Kuduva et al., 1999) – which themselves are uncommon – and, of course, it never occurs in carboxyl dimers, which are necessarily cisoid. This exceptional aggregation does not appear to be due to any obvious feature of the geometry of (I), whose structure and stereochemistry resemble those of the other 5β steroids we have reported (Thompson et al., 2001; Kikolski, Davison et al., 2006; Kikolski, Lalancette et al., 2006).
Fig. 2 shows the packing of (I). All hydrogen bonding occurs in an acid-to-acid catemer arrangement, whose screw-related components advance in the [100] direction along the ab face, while a second chain proceeds counterdirectionally a half-cell away in c. These two catemers interleave at their remote ends, with their ketone dipoles opposing to utilize attractive dipolar interactions. The ketone carbonyl groups, which have no part in the hydrogen bonding, are not fully parallel; thus the intermolecular C···O stacking distance is 4.409 (3) Å at one end and 4.962 (3) Å at the other end, yielding a dihedral angle of 29.26 (5)° between adjacent ketone planes C2/C3/C4/O1 versus C2'/C3'/C4'/O1'(−x + 1, y + 1/2, −z + 3/2).
We characterize the geometry of hydrogen bonding to carbonyl groups using a combination of H···O═C angle and H···O═C—C or H···O═C—C—O torsion angle. These describe the approach of the acid H atom to the receptor O in terms of its deviation from, respectively, C═O axiality (ideal 120°) and planarity with the carbonyl group (ideal 0°). In practice, experimental values for these two quantities cluster strongly around their theoretically ideal angles, so that deviation from them may be used as a rough index of strain in the hydrogen-bonding arrangement. In (I), the angles in question are H3···O2—C23, whose value is 128.7 (10)°, and H3···O2—C23—O3, whose value is 16.6 (12)°. In the two other known instances of anti–anti acid-to-acid catemerization (see below), the corresponding angles are 120.9 and 10.5°, respectively (Bryan & White, 1982), and 117.6 and 0.0°, respectively (Wiechert et al., 1997).
Within the 2.6 Å range surveyed for nonbonded intermolecular C—H···O packing interactions, only one close contact exists (see Table 2). However, this contact involves donation toward O3 from a methylene H atom (H22A) directly adjacent to the carboxyl group that is donating its acid hydrogen to O2 in the anti hydrogen bond (Fig. 2). This creates a ladder-like set of connections that clearly plays a significant role in stabilizing the hydrogen bonding, although it is not clear why it would function less well in the tautomeric syn–syn arrangement.
The rarity of acid-to-acid catemers, of either syn or anti carboxyl conformation, diminishes significantly when dimerization is suppressed by precluding centrosymmetric modes. Even so, (I) is only the third instance we have found of any such catemer in a keto acid (Lalancette et al., 1998; Zinczuk et al., 2004). Although our H-atom placement in (I) is dictated by its ordered C—O bond lengths, an extended tautomeric H-atom shift along the chain can be envisioned for (I) that, with appropriate resizing of the C—O bonds, would yield an alternative all-syn catemer. However, unless some C atoms are shifted as well, the result appears to produce geometrically unfavorable C—O—H angles, and we have found no evidence for such an alternative species or for any disorder created by such a process, either static or dynamic. We attempted to force such a syn conformer on our asymmetric unit, but the refinement could not be improved beyond R[F2>2σ(F2)] = 0.08.
Historically, Leiserowitz (1976), working from a very modest 25 000 or so X-ray structures (CCDC, 2000), concluded that only carboxyl groups involved in intramolecular hydrogen bonding display the antiplanar conformation. This remains nearly correct, despite the present availability of a vastly expanded structural database. The first `exception', an acid-to-amide catemer, appears to have been that of Fujinaga & James (1980). Since then, additional examples have gradually accumulated, but the percentage of non-intramolecular antiplanar-carboxyl structures remains minute. Desiraju and his collaborators (Desiraju et al., 1990; Goud & Desiraju, 1993; Das et al., 2003, 2005; Das & Desiraju, 2006) have published several examples of alternating syn–anti catemer formations in phenylpropiolic acids and cubanecarboxylic acids. Among these papers, Kuduva et al. (1999) reported that their search of the 181 309 entries in the 1998 Cambridge Structural Database found a total of 73 acid-to-acid catemers, of which four were combined syn–anti arrangements and only two represented all-anti species. Our own search of the 390 081 entries in the current database (Cambridge Structural Database; Version 5.28, update of November, 2006; Allen, 2002) has found a total of 153 acid-to-acid catemers, of which the number of anti–anti instances remains at only two (Bryan & White, 1982; Wiechert et al., 1997).
Because some all-anti and all-syn catemers are tautomerically related, as described above, and yet the anti species is so rarely observed, the clear inference is that anti conformations are energetically disfavored. While much interest has therefore focused on the energy difference involved, experimental data seem to be derived entirely from formic acid, and computational results have seldom extended much further. For the most part, ΔGsyn/anti values found for vapor-phase formic acid lie in the 8.5–16.5 kJ mol−1 range (Miyazawa & Pitzer, 1959; Lide, 1964, 1966; Hocking, 1976); however, Pawar et al. (2007) have recently reported a ΔGsyn/anti for formic acid of ca 3.8 kJ mol−1 in a solution that permitted hydrogen bonding but suppressed dimerization. The computational values for ΔGsyn/anti generally fall in the range 19–26.5 kJ mol−1 (Radom et al., 1972; Allinger & Chang, 1977; Peterson & Csizmadia, 1979; Wiberg & Laidig, 1987), and the few values calculated for acetic and propionic acids are higher than the formic acid values by a few kJ mol−1. The range of values estimated by Gandour (1981) from kinetic data in enzyme models (ca 6–23 kJ mol−1) may seem unhelpfully broad, but these represent a variety of acids larger and more complex than formic. The applicability of any of these estimates to the crystalline state is unclear.
Such ΔG values have been accepted in varying degrees and sometimes cited as though they might represent carboxylic acids other than those actually employed in the experiments or calculations performed. Such a notion is easily dispelled by considering cases like 1-carboxybicyclo[2.2.2]octane, where any anti conformation must be impossibly hindered. What seems clear is that a range of ΔGsyn/anti values exists, with formic acid at or near one end, since the substituent sterically opposed to acid-H in its anti conformer is the least demanding one possible. Values of ΔGsyn/anti probably correlate generally with steric bulk and degree of substitution at the acid's Cα atom [cf. Newman's `rule of six' (Newman, 1950, 1956)], and bond polarities may well also play a part. What we may presumably take as proven is that, when instances of anti-carboxyl hydrogen bonding appear, whatever ΔG disadvantage there is to an anti conformation is better than no hydrogen bond at all, although what maximum this places on ΔGsyn/anti is rather difficult to estimate, given the widely varying values offered in the literature for O—H···O bond strength.