The crystal structure of Ti
2P has been analysed using electron diffraction and high-resolution electron-microscopy techniques. A new unit cell was found, the compound is hexagonal with
a = 19.969 (1) and
c = 3.4589 (1) Å. The structure was first solved in space group
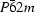
in projection using direct methods on electron diffraction data from the [001] zone axis. A three-dimensional solution was obtained using again direct methods but on a three-dimensional set of electron diffraction data recorded with the precession technique. Ti
2P is a distorted Fe
2P structure and, based on high-resolution images, it is possible to explain that the tripling of the unit cell is due to the ordering of P vacancies that reduces the symmetry to
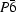
.
Supporting information
Data collection: QED (Belletti, Calestani, Gemmi, Migliori, Ultramicroscopy, 2000, 81, 57-65)
CRISP (Hovmöller, Ultramicroscopy, 1992, 41, 121-125); cell refinement: GSAS (Larson and Von Dreele 1994); program(s) used to solve structure: SIR97(Cascarano al.,Acta Cryst.,1996,A52,C-79).
Crystal data top
| Ti2P | c = 3.4589 (1) Å |
| Mr = 3421.81 | V = 1194.5 (1) Å3 |
| Hexagonal, P62m | Z = 27 |
| a = 19.969 (1) Å | T = 295 K |
Data collection top
Philips CM30T
diffractometer | Rint = 0.22 |
| Radiation source: thermoionic electron gun | h = 0→15 |
| precessed electron diffraction scans | k = −7→0 |
| 98 measured reflections | l = 0→2 |
Special details top
Experimental. Structure solved by electron diffraction data collected with precession
tecnique·Microscope used: Philps CM30T Accelerating voltage 300 kV |
Refinement. The structure was solved using direct methods on precessed electron diffraction
data. Because of the dynamical effects the quality of the data did not allowed
the structure refinement. The errors reported in the atomic positions are just
an estimate calculated on the basis of one cycle of refinement. |
Fractional atomic coordinates and isotropic or equivalent isotropic displacement parameters (Å2) top| | x | y | z | Biso*/Beq | |
| TI1 | 0.427 (6) | 0.093 (6) | 0.5000 | | |
| TI2 | 0.239 (8) | 0.0000 | 0.5000 | | |
| TI3 | 0.330 (6) | 0.133 (6) | 0.0000 | | |
| TI4 | 0.472 (8) | 0.0000 | 0.0000 | | |
| TI5 | 0.098 (8) | 0.098 (8) | 0.5000 | | |
| TI6 | 0.755 (5) | 0.424 (7) | 0.5000 | | |
| TI7 | 0.136 (8) | 0.0000 | 0.0000 | | |
| TI8 | 0.878 (6) | 0.545 (6) | 0.0000 | | |
| TI9 | 0.800 (7) | 0.330 (8) | 0.0000 | | |
| TI10 | 0.206 (6) | 0.206 (6) | 0.0000 | | |
| TI11 | 1.0000 | 0.590 (7) | 0.5000 | | |
| TI12 | 0.335 (6) | 0.245 (6) | 0.5000 | | |
| P1 | 0.6667 | 0.3333 | 0.0000 | | |
| P2 | 0.0000 | 0.0000 | 0.0000 | | |
| P3 | 0.33 (1) | 0.0000 | 0.0000 | | |
| P4 | 0.444 (7) | 0.23 (1) | 0.5000 | | |
| P5 | 0.225 (7) | 0.117 (9) | 0.5000 | | |
| P6 | 0.55 (1) | 0.108 (7) | 0.5000 | | |
| P7 | 0.328 (10) | 0.328 (10) | 0.0000 | | |
Bond lengths (Å) top
| TI1—TI1i | 3.21 (15) | P3—TI1 | 2.57 (10) |
| TI1—TI2 | 3.3 (2) | P3—TI3 | 2.66 (16) |
| TI1—TI3 | 2.99 (17) | P3—TI4 | 2.8 (3) |
| TI1—TI4 | 2.99 (15) | P4—TI6v | 2.4 (3) |
| TI1—TI9ii | 2.72 (10) | P4—TI12 | 2.3 (2) |
| TI2—TI3 | 2.92 (8) | P4—TI1 | 2.6 (2) |
| TI2—TI7 | 2.69 (17) | P4—TI8vii | 2.61 (17) |
| TI3—TI12 | 2.79 (14) | P4—TI9ii | 2.70 (19) |
| TI4—TI11iii | 2.92 (14) | P4—TI3 | 2.74 (11) |
| TI5—TI5iv | 3.4 (2) | P5—TI2 | 2.5 (2) |
| TI5—TI7 | 2.98 (18) | P5—TI3 | 2.61 (15) |
| TI5—TI10 | 2.76 (11) | P5—TI5 | 2.4 (2) |
| TI6—TI6ii | 3.10 (17) | P5—TI7 | 2.73 (10) |
| TI6—TI8 | 2.99 (9) | P5—TI10 | 2.64 (19) |
| TI6—TI9 | 3.00 (19) | P5—TI12 | 2.40 (14) |
| TI6—TI9v | 2.87 (18) | P6—TI1 | 2.3 (2) |
| TI8—TI11 | 2.75 (8) | P6—TI4 | 2.59 (8) |
| TI8—TI12iii | 2.76 (13) | P6—TI6ii | 2.57 (14) |
| TI10—TI12 | 2.87 (14) | P6—TI8ii | 2.81 (19) |
| TI11—TI12ii | 2.86 (19) | P6—TI9ii | 2.69 (19) |
| TI12—TI12vi | 3.1 (2) | P6—TI11ii | 2.7 (2) |
| P1—TI6 | 2.49 (6) | P7—TI8v | 2.5 (3) |
| P1—TI9 | 2.71 (16) | P7—TI10 | 2.47 (17) |
| P2—TI5 | 2.61 (8) | P7—TI11v | 2.35 (10) |
| P2—TI7 | 2.72 (16) | P7—TI12 | 2.46 (19) |
| P3—TI2 | 2.51 (18) | | |
| Symmetry codes: (i) x−y, −y, −z+1; (ii) −x+y+1, −x+1, −z+1; (iii) −x+y+1, −x+1, −z; (iv) −x+y, −x, −z+1; (v) −y+1, x−y, z; (vi) y, x, −z+1; (vii) −y+1, x−y, z+1. |

 journal menu
journal menu











