The tricalcium dimanganese heptaoxide (Ca
3Mn
2O
7) member of the Ruddlesden–Popper series Ca
n+1Mn
nO
3n+1,
i.e. with
n = 2, was previously reported with an
I-centred tetragonal lattice [
at = 3.68 and
ct = 19.57 Å] by Fawcett, Sunstrom, Greenblatt, Croft & Ramanujachary [
Chem. Mater. (1998),
10, 3643–3651]. It is now found to be orthorhombic, with an
A-centred lattice [
a = 5.2347 (6),
b = 5.2421 (2) and
c = 19.4177 (19) Å]. The structure has been refined in space group
A2
1am using X-ray single-crystal diffraction data and assuming the existence of twin domains related by the (1
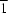
0) plane. A comparison with the basic perovskite structure CaMnO
3 (
n = ∞) is proposed.
Supporting information
The initial sample preparation consisted of a mixture of CaO, prepared by
decarbonation of CaCO3 at 1273 K, and MnO2 (Aldrich) in stoichiometric
proportions, to produce CaMnO3. The mixture was heated to 1273 K and then
crushed three times in succession Query, so as to obtain a good sample
homogeneity, and was then compressed in an isostatic press at 3 × 10 7
Pa (is this the correct conversion from 3 tons/cm2? Are metric tonnes
intended?) in the form of a rod 5 × 50 mm, before sintering at 1673 K
for 12 h in air. Crystal growth was carried out in a four-mirror optical
floating-zone furnace (Crystal Systems Inc. FZT 10000 H III P). The samples
were set to rotate in opposite directions at 20 revolutions per minute and
were grown in an oxygen flow at atmospheric pressure, at a feeding speed of 10 mm/h. It is noteworthy to state that the previous ceramic synthesis of
Ca3Mn2O7 could only be performed under a high pressure of oxygen (3200
psi; 1 psi ≈ 6.895 × 10 3 Pa) (MacChesney et al., 1967).
Data collection: CAD-4 Software (Enraf-Nonius, 1994); cell refinement: CAD-4 Software; data reduction: JANA2000 (Petříček & Dušek, 2000); program(s) used to solve structure: Please provide missing details; program(s) used to refine structure: JANA2000; molecular graphics: ATOMS (Dowty, 1997); software used to prepare material for publication: JANA2000.
tricalcium dimanganese heptaoxide
top
Crystal data top
| Ca3Mn2O7 | Dx = 4.266 Mg m−3 |
| Mr = 342.1 | Mo Kα radiation, λ = 0.71073 Å |
| Orthorhombic, A21am | Cell parameters from 25 reflections |
| a = 5.2347 (6) Å | θ = 11.0–24.0° |
| b = 5.2421 (2) Å | µ = 7.61 mm−1 |
| c = 19.4177 (19) Å | T = 298 K |
| V = 532.83 (8) Å3 | Prism, black |
| Z = 4 | 0.12 × 0.07 × 0.02 mm |
| F(000) = 664 | |
Data collection top
Enraf-nonius CAD-4
diffractometer | Rint = 0.045 |
| θ/2θ scans | θmax = 50.0°, θmin = 2.1° |
Absorption correction: gaussian
(JANA2000; Petříček & Dušek, 2000) | h = −11→11 |
| Tmin = 0.619, Tmax = 0.865 | k = −11→11 |
| 10766 measured reflections | l = −41→41 |
| 1516 independent reflections | 3 standard reflections every 60 min |
| 745 reflections with I > 3σ(I) | intensity decay: 0.2% |
Refinement top
| Refinement on F | Weighting scheme based on measured s.u.'s w = 1/σ2(F) |
| R[F2 > 2σ(F2)] = 0.023 | (Δ/σ)max < 0.001 |
| wR(F2) = 0.015 | Δρmax = 1.39 e Å−3 |
| S = 1.45 | Δρmin = −1.13 e Å−3 |
| 1516 reflections | Absolute structure: (Flack, 1983) |
| 59 parameters | Absolute structure parameter: 0.45 (6) |
Crystal data top
| Ca3Mn2O7 | V = 532.83 (8) Å3 |
| Mr = 342.1 | Z = 4 |
| Orthorhombic, A21am | Mo Kα radiation |
| a = 5.2347 (6) Å | µ = 7.61 mm−1 |
| b = 5.2421 (2) Å | T = 298 K |
| c = 19.4177 (19) Å | 0.12 × 0.07 × 0.02 mm |
Data collection top
Enraf-nonius CAD-4
diffractometer | 745 reflections with I > 3σ(I) |
Absorption correction: gaussian
(JANA2000; Petříček & Dušek, 2000) | Rint = 0.045 |
| Tmin = 0.619, Tmax = 0.865 | 3 standard reflections every 60 min |
| 10766 measured reflections | intensity decay: 0.2% |
| 1516 independent reflections | |
Refinement top
| R[F2 > 2σ(F2)] = 0.023 | Δρmax = 1.39 e Å−3 |
| wR(F2) = 0.015 | Δρmin = −1.13 e Å−3 |
| S = 1.45 | Absolute structure: (Flack, 1983) |
| 1516 reflections | Absolute structure parameter: 0.45 (6) |
| 59 parameters | |
Fractional atomic coordinates and isotropic or equivalent isotropic displacement parameters (Å2) top| | x | y | z | Uiso*/Ueq | |
| Mn | 0.3033 (7) | 0.2507 (3) | 0.098160 (10) | 0.0185 (4) | |
| Ca1 | 0.8276 (8) | 0.2505 (5) | 0.0 | 0.0383 (10) | |
| Ca2 | 0.7907 (8) | 0.2457 (3) | 0.18642 (2) | 0.0386 (8) | |
| O1 | 0.3031 (7) | 0.2937 (4) | 0.0 | 0.051 (5) | |
| O2 | 0.0954 (9) | 0.9618 (6) | 0.08924 (8) | 0.024 (4) | |
| O3 | 0.0221 (9) | 0.4649 (6) | 0.10545 (9) | 0.041 (5) | |
| O4 | 0.3101 (10) | 0.2176 (4) | 0.19583 (5) | 0.051 (5) | |
Atomic displacement parameters (Å2) top| | U11 | U22 | U33 | U12 | U13 | U23 |
| Mn | 0.00362 (9) | 0.00376 (10) | 0.00390 (6) | 0.0004 (3) | 0.00067 (11) | 0.0001 (2) |
| Ca1 | 0.0071 (4) | 0.0078 (2) | 0.00703 (14) | −0.0025 (8) | 0.0 | 0.0 |
| Ca2 | 0.00889 (18) | 0.00776 (19) | 0.00520 (8) | −0.0017 (6) | 0.00032 (16) | 0.0007 (3) |
| O1 | 0.0106 (10) | 0.0103 (12) | 0.0045 (4) | 0.0011 (16) | 0.0 | 0.0 |
| O2 | 0.0037 (8) | 0.0049 (9) | 0.0103 (6) | −0.0017 (5) | 0.0010 (6) | −0.0019 (6) |
| O3 | 0.0066 (9) | 0.0084 (11) | 0.0121 (6) | 0.0028 (6) | 0.0013 (8) | −0.0007 (8) |
| O4 | 0.0093 (7) | 0.0104 (11) | 0.0044 (4) | −0.0003 (12) | 0.0011 (9) | 0.0007 (3) |
Geometric parameters (Å, º) top
| Mn—O1 | 1.9193 (4) | Ca1—O3iii | 2.548 (3) |
| Mn—O2i | 1.873 (4) | Ca1—O3v | 2.996 (4) |
| Mn—O2ii | 1.900 (5) | Ca1—O3viii | 2.548 (3) |
| Mn—O3 | 1.857 (5) | Ca1—O3ii | 2.996 (4) |
| Mn—O3ii | 1.885 (4) | Ca2—O2vi | 2.884 (4) |
| Mn—O4 | 1.9048 (10) | Ca2—O2ii | 2.406 (3) |
| Ca1—O1 | 2.755 (5) | Ca2—O3iii | 2.293 (4) |
| Ca1—O1iii | 2.499 (5) | Ca2—O3ii | 2.598 (4) |
| Ca1—O1iv | 2.856 (3) | Ca2—O4 | 2.526 (4) |
| Ca1—O1v | 2.393 (3) | Ca2—O4iii | 2.730 (4) |
| Ca1—O2vi | 2.694 (4) | Ca2—O4ix | 2.2968 (11) |
| Ca1—O2v | 2.391 (3) | Ca2—O4x | 2.438 (2) |
| Ca1—O2vii | 2.694 (4) | Ca2—O4ii | 2.821 (2) |
| Ca1—O2ii | 2.391 (3) | | |
| | | |
| O1—Mn—O2i | 90.16 (12) | O3iii—Ca2—O4x | 121.90 (14) |
| O1—Mn—O2ii | 88.78 (14) | O3iii—Ca2—O4ii | 61.68 (9) |
| O1—Mn—O3 | 90.24 (14) | O3ii—Ca2—O4 | 62.55 (13) |
| O1—Mn—O3ii | 88.97 (13) | O3ii—Ca2—O4iii | 127.68 (14) |
| O1—Mn—O4 | 178.15 (18) | O3ii—Ca2—O4ix | 125.28 (13) |
| O2i—Mn—O2ii | 89.15 (19) | O3ii—Ca2—O4x | 130.52 (13) |
| O2i—Mn—O3 | 92.0 (2) | O3ii—Ca2—O4ii | 58.43 (8) |
| O2i—Mn—O3ii | 177.9 (2) | O4—Ca2—O4iii | 169.74 (6) |
| O2i—Mn—O4 | 91.69 (10) | O4—Ca2—O4 | 88.69 (10) |
| O2ii—Mn—O2i | 89.15 (19) | O4—Ca2—O4x | 88.75 (11) |
| O2ii—Mn—O3 | 178.48 (18) | O4—Ca2—O4ii | 95.13 (11) |
| O2ii—Mn—O3ii | 88.9 (2) | O4iii—Ca2—O4ix | 83.89 (10) |
| O2ii—Mn—O4 | 91.27 (12) | O4iii—Ca2—O4x | 84.23 (11) |
| O3—Mn—O3ii | 89.87 (19) | O4iii—Ca2—O4ii | 90.77 (10) |
| O3—Mn—O4 | 89.67 (11) | O4ix—Ca2—O4x | 90.40 (7) |
| O3ii—Mn—O4 | 89.19 (11) | O4ix—Ca2—O4ii | 81.40 (7) |
| O1—Ca1—O1iii | 170.09 (13) | O4x—Ca2—O4ii | 170.82 (9) |
| O1—Ca1—O1iv | 92.14 (14) | Mn—O1—Mnxi | 166.51 (14) |
| O1—Ca1—O1v | 82.21 (14) | Mn—O1—Ca1xii | 89.42 (15) |
| O1—Ca1—O2vi | 124.39 (13) | Mn—O1—Ca1xiii | 83.26 (8) |
| O1—Ca1—O2v | 62.08 (14) | Mn—O1—Ca1xiv | 96.73 (8) |
| O1—Ca1—O3iii | 111.22 (14) | Ca1xii—O1—Ca1 | 170.09 (12) |
| O1—Ca1—O3v | 55.05 (11) | Ca1xii—O1—Ca1xiii | 87.38 (13) |
| O1iii—Ca1—O1iv | 97.77 (14) | Ca1xii—O1—Ca1xiv | 98.27 (16) |
| O1iii—Ca1—O1v | 87.87 (15) | Ca1—O1—Ca1xiii | 82.71 (13) |
| O1iii—Ca1—O2vi | 62.14 (13) | Ca1—O1—Ca1xiv | 91.64 (15) |
| O1iii—Ca1—O2v | 123.25 (14) | Ca1xiii—O1—Ca1xiv | 174.4 (2) |
| O1iii—Ca1—O3iii | 64.03 (13) | Ca1xiv—O1—Ca1xii | 98.27 (16) |
| O1iv—Ca1—O1 | 92.14 (14) | Ca1xiv—O1—Ca1 | 91.64 (15) |
| O1iv—Ca1—O1v | 174.4 (2) | Mnxv—O2—Mnxvi | 159.0 (2) |
| O1iv—Ca1—O2vi | 57.47 (10) | Mnxv—O2—Ca1xvii | 84.70 (14) |
| O1iv—Ca1—O2v | 60.81 (10) | Mnxv—O2—Ca1xiv | 98.5 (2) |
| O1iv—Ca1—O3iii | 117.30 (10) | Mnxv—O2—Ca2xvii | 81.00 (14) |
| O1iv—Ca1—O3v | 118.26 (12) | Mnxv—O2—Ca2xvi | 92.64 (16) |
| O1v—Ca1—O2vi | 126.07 (13) | Mnxvi—O2—Ca1xvii | 88.24 (18) |
| O1v—Ca1—O2v | 115.94 (14) | Mnxvi—O2—Ca1xiv | 101.67 (15) |
| O1v—Ca1—O3iii | 65.23 (10) | Mnxvi—O2—Ca2xvii | 78.33 (15) |
| O1v—Ca1—O3v | 58.27 (10) | Mnxvi—O2—Ca2xvi | 90.31 (14) |
| O2vi—Ca1—O2v | 117.98 (14) | Ca1xvii—O2—Ca1xiv | 93.43 (9) |
| O2vi—Ca1—O2vii | 80.06 (13) | Ca1xvii—O2—Ca2xvii | 80.98 (12) |
| O2vi—Ca1—O2ii | 62.42 (14) | Ca1xvii—O2—Ca2xvi | 168.37 (15) |
| O2vi—Ca1—O3iii | 61.51 (11) | Ca1xiv—O2—Ca2xvii | 174.41 (15) |
| O2vi—Ca1—O3v | 175.61 (12) | Ca1xiv—O2—Ca2xvi | 98.16 (17) |
| O2vi—Ca1—O3viii | 123.8 (2) | Ca2xvii—O2—Ca2xvi | 87.43 (9) |
| O2vi—Ca1—O3ii | 96.77 (8) | Mn—O3—Mnxvi | 162.6 (2) |
| O2v—Ca1—O2ii | 92.87 (16) | Mn—O3—Ca1xii | 89.36 (14) |
| O2v—Ca1—O3iii | 172.2 (2) | Mn—O3—Ca1xiv | 79.97 (15) |
| O2v—Ca1—O3v | 57.67 (11) | Mn—O3—Ca2xii | 99.67 (16) |
| O2v—Ca1—O3viii | 79.98 (11) | Mn—O3—Ca2xvi | 88.29 (19) |
| O2v—Ca1—O3ii | 117.1 (2) | Mnxvi—O3—Ca1xii | 92.62 (16) |
| O2ii—Ca1—O3iii | 79.98 (11) | Mnxvi—O3—Ca1xiv | 83.06 (13) |
| O3iii—Ca1—O3v | 122.88 (13) | Mnxvi—O3—Ca2xii | 97.3 (2) |
| O3iii—Ca1—O3viii | 106.95 (16) | Mnxvi—O3—Ca2xvi | 84.98 (14) |
| O3iii—Ca1—O3ii | 56.25 (13) | Ca1xii—O3—Ca1xiv | 83.32 (9) |
| O3v—Ca1—O3ii | 86.23 (12) | Ca1xii—O3—Ca2xii | 96.83 (16) |
| O2vi—Ca2—O2ii | 59.24 (13) | Ca1xii—O3—Ca2xvi | 163.76 (16) |
| O2vi—Ca2—O3iii | 61.18 (12) | Ca1xiv—O3—Ca2xii | 179.6 (2) |
| O2vi—Ca2—O3ii | 101.81 (9) | Ca1xiv—O3—Ca2xvi | 80.44 (12) |
| O2vi—Ca2—O4 | 124.60 (12) | Ca2xii—O3—Ca2xvi | 99.41 (9) |
| O2vi—Ca2—O4iii | 57.66 (11) | Mn—O4—Ca2xii | 84.81 (11) |
| O2vi—Ca2—O4ix | 132.06 (15) | Mn—O4—Ca2 | 86.65 (11) |
| O2vi—Ca2—O4x | 60.78 (8) | Mn—O4—Ca2xviii | 169.33 (13) |
| O2vi—Ca2—O4ii | 122.47 (12) | Mn—O4—Ca2xix | 90.88 (8) |
| O2ii—Ca2—O3iii | 85.02 (11) | Mn—O4—Ca2xvi | 81.02 (8) |
| O2ii—Ca2—O3ii | 63.86 (12) | Ca2xii—O4—Ca2 | 169.74 (7) |
| O2ii—Ca2—O4 | 66.88 (14) | Ca2xii—O4—Ca2xii | 91.02 (11) |
| O2ii—Ca2—O4iii | 116.84 (15) | Ca2xii—O4—Ca2xix | 90.40 (11) |
| O2ii—Ca2—O4ix | 146.87 (16) | Ca2xii—O4—Ca2xvi | 84.60 (10) |
| O2ii—Ca2—O4x | 68.05 (9) | Ca2—O4—Ca2xviii | 96.39 (11) |
| O2ii—Ca2—O4ii | 121.13 (10) | Ca2—O4—Ca2xix | 95.41 (12) |
| O3iii—Ca2—O3ii | 65.07 (14) | Ca2—O4—Ca2xvi | 88.46 (10) |
| O3iii—Ca2—O4 | 127.21 (15) | Ca2xviii—O4—Ca2xix | 98.99 (7) |
| O3iii—Ca2—O4iii | 63.05 (15) | Ca2xviii—O4—Ca2xvi | 88.82 (7) |
| O3iii—Ca2—O4ix | 128.10 (16) | Ca2xix—O4—Ca2xvi | 170.82 (7) |
| Symmetry codes: (i) x, y−1, z; (ii) x+1/2, −y+1, z; (iii) x+1, y, z; (iv) x+1/2, −y, −z; (v) x+1/2, −y+1, −z; (vi) x+1, y−1, z; (vii) x+1, y−1, −z; (viii) x+1, y, −z; (ix) x+1/2, −y+1/2, −z+1/2; (x) x+1/2, −y, z; (xi) x, y, −z; (xii) x−1, y, z; (xiii) x−1/2, −y, −z; (xiv) x−1/2, −y+1, −z; (xv) x, y+1, z; (xvi) x−1/2, −y+1, z; (xvii) x−1, y+1, z; (xviii) x−1/2, −y+1/2, −z+1/2; (xix) x−1/2, −y, z. |
Experimental details
| Crystal data |
| Chemical formula | Ca3Mn2O7 |
| Mr | 342.1 |
| Crystal system, space group | Orthorhombic, A21am |
| Temperature (K) | 298 |
| a, b, c (Å) | 5.2347 (6), 5.2421 (2), 19.4177 (19) |
| V (Å3) | 532.83 (8) |
| Z | 4 |
| Radiation type | Mo Kα |
| µ (mm−1) | 7.61 |
| Crystal size (mm) | 0.12 × 0.07 × 0.02 |
| |
| Data collection |
| Diffractometer | Enraf-nonius CAD-4
diffractometer |
| Absorption correction | Gaussian
(JANA2000; Petříček & Dušek, 2000) |
| Tmin, Tmax | 0.619, 0.865 |
No. of measured, independent and
observed [I > 3σ(I)] reflections | 10766, 1516, 745 |
| Rint | 0.045 |
| (sin θ/λ)max (Å−1) | 1.077 |
| |
| Refinement |
| R[F2 > 2σ(F2)], wR(F2), S | 0.023, 0.015, 1.45 |
| No. of reflections | 1516 |
| No. of parameters | 59 |
| No. of restraints | ? |
| Δρmax, Δρmin (e Å−3) | 1.39, −1.13 |
| Absolute structure | (Flack, 1983) |
| Absolute structure parameter | 0.45 (6) |
Selected bond lengths (Å) top| Mn—O1 | 1.9193 (4) | Ca1—O3iii | 2.548 (3) |
| Mn—O2i | 1.873 (4) | Ca1—O3v | 2.996 (4) |
| Mn—O2ii | 1.900 (5) | Ca1—O3viii | 2.548 (3) |
| Mn—O3 | 1.857 (5) | Ca1—O3ii | 2.996 (4) |
| Mn—O3ii | 1.885 (4) | Ca2—O2vi | 2.884 (4) |
| Mn—O4 | 1.9048 (10) | Ca2—O2ii | 2.406 (3) |
| Ca1—O1 | 2.755 (5) | Ca2—O3iii | 2.293 (4) |
| Ca1—O1iii | 2.499 (5) | Ca2—O3ii | 2.598 (4) |
| Ca1—O1iv | 2.856 (3) | Ca2—O4 | 2.526 (4) |
| Ca1—O1v | 2.393 (3) | Ca2—O4iii | 2.730 (4) |
| Ca1—O2vi | 2.694 (4) | Ca2—O4ix | 2.2968 (11) |
| Ca1—O2v | 2.391 (3) | Ca2—O4x | 2.438 (2) |
| Ca1—O2vii | 2.694 (4) | Ca2—O4ii | 2.821 (2) |
| Ca1—O2ii | 2.391 (3) | | |
| Symmetry codes: (i) x, y−1, z; (ii) x+1/2, −y+1, z; (iii) x+1, y, z; (iv) x+1/2, −y, −z; (v) x+1/2, −y+1, −z; (vi) x+1, y−1, z; (vii) x+1, y−1, −z; (viii) x+1, y, −z; (ix) x+1/2, −y+1/2, −z+1/2; (x) x+1/2, −y, z. |

 journal menu
journal menu








![[Figure 1]](http://journals.iucr.org/c/issues/2002/01/00/gd1169/gd1169fig1thm.gif)
![[Figure 2]](http://journals.iucr.org/c/issues/2002/01/00/gd1169/gd1169fig2thm.gif)




In order to complete magnetic and electrical measurements on the magnetoresistive manganese oxide perovskite families Ln1 - xCaxMnO3 (Ln is a rare earth), a structural study of these compounds has been developed, including the end compound CaMnO3 (x = 1). From the same CaMnO3 preparation, single crystals of a second compound were isolated, exhibiting cell parameters clearly different from those known for CaMnO3 (Poeppelmeier et al., 1982; Taguchi et al., 1989; Aliaga et al., 2000). Scanning electron microscopy measurements, coupled with EDS (please define) analysis, clearly lead to a Ca3Mn2 cationic composition.
The cell parameters of Ca3Mn2O7 are consistent with either an orthorhombic or a tetragonal lattice. They depend both on the ap cubic parameter (ap = 3.72 Å) of the basic CaMnO3 perovskite cell, with CaMnO3 representing the n = ∞ member of the Ruddlesden-Popper series (Ruddlesden & Popper, 1958), and on the face-centred cubic cell of CaO {aO = 4.8 Å [Tanida & Kitamura, 1981; ref. 41–0421, International Centre for Diffraction Data (ICDD, 1999)]}. The parameters found in the present work differ from those previously published for Ca3Mn2O7 (at ≈ ap, ct ≈ 4ap + 2aO) (MacChesney et al., 1967; Tanida & Kitamura, 1981; Fawcett et al., 1998) by the relation a ≈ b ≈ at21/2, c ≈ ct.
The symmetry of the present crystal was carefully scrutinized from both Laue diagrams (precession camera) and the intensity distribution in the X-ray diffraction data. The actual Laue symmetry is mmm rather than 4/mmm, as shown by the Laue diffraction pattern, and is confirmed from the Rint values of 4.49% and 9.73% calculated assuming orthorhombic and tetragonal symmetry, respectively. Moreover, some significant reflections of the type hkl, where h + k = 2n + 1, were observed and cannot be explained in the tetragonal model.
The present reflection conditions are consistent with the centrosymmetric space group Amam, but a satisfactory R factor could not be obtained with this symmetry. A new solution could be initiated using the direct method calculation program SIR97 (Altomare et al., 1999) in the non-centrosymmetric space group A21am (No 36). The standard setting of this group is Cmc21, but we adopted the non-standard setting in order to keep the pseudo-tetragonal cell along the c axis. This space group has already been proposed for the Ca3Ti2O7 structure by Elcombe et al. (1991) and for La2–2xCa1 + 2xMn2O7 by Bendersky et al. (2001).
The atomic positions were refined to R = 0.0228 using the JANA2000 structural refinement program (Petříček & Dušek, 2000) with anisotropic displacement parameters for all the atoms and assuming the existence of twin domains related by the (110) plane, due to the similarity between the a and b parameters, with reference to a pseudo-tetragonal cell. The twin ratio was found to be equal to 0.18. This twin model leads to a significant improvement of the R-factor (0.0317 without a twin).
The corresponding structure, with Ca1 and O1 atoms in 4a crystallographic sites and the other atoms in 8 b sites, is shown in Fig. 1a. It consists of a stacking of two layers formed by corner-sharing MnO6 octahedra, separated by a double Ca—O layer. This description is consistent with the usual description of the Ruddlesden-Popper Can+1MnnO3n+1 family, which can also be represented by the formula CaO[CaMnO3]n, where n is the number of MnO6 octahedra layers.
Three types of polyhedra are present in this structure, one per cation, i.e. Mn4+, Ca12+ and Ca22+. The Mn4+ ions are octahedrally coordinated, and the Mn—O bond distances in the equatorial plane range from 1.856 (5) to 1.899 (5) Å, with apical distances of 1.904 (1) and 1.9193 (4) Å. The corresponding average Mn—O distance is 1.890 (3) Å. Angles within the MnO6 octahedra range from 88.7 (1) to 92.0 (2)° for O—Mn—O with cis O atoms, and from 177.9 (2) to 178.4 (1)° for O—Mn—O with trans O atoms.
Comparing the MnO6 octahedra in Ca3Mn2O7 with those in CaMnO3 (Poeppelmeier et al., 1982), we note that the Mn—O distances in the equatorial plane of the octahedra are shorter in Ca3Mn2O7, while the apical distances are larger, leading to an elongated octahedron in Ca3Mn2O7 instead of a compressed one in CaMnO3 (1.865 Å for the apical distances, and 1.900 and 1.903 Å for the equatorial ones).
The atoms Ca12+, at z = 0 and z = 1/2, are 12-fold coordinated (usual perovskite coordination), while the atoms Ca22+ are ninefold coordinated. Both Ca1 and Ca2 atoms belong to similar CaO layers orthogonal to c. The O—O distances in these layers, represented by dashed lines in Fig. 1 b, clearly show the difference from tetragonal symmetry, due to the MnO6 octahedral distortion and tilting, which are forbidden in tetragonal symmetry. This projection clearly shows the analogy with the actual Pnma symmetry of the CaMnO3 structure.
The average Ca—O distances are 2.646 (4) Å for the Ca1 polyhedra and 2.554 (3) Å for the Ca2 polyhedra, whereas the average Ca—O distance in CaMnO3 is 2.652 Å. Two short Ca2—O distances (<2.3 Å) are observed (Table 1). The average Mn—O and Ca—O distances are in good agreement with those predicted by the ionic radii calculated by Shannon (1976), with rMn4+ = 0.53, rCa(1)2+ = 1.34, rCa(2)2+ = 1.18 and rO2- = 1.35 Å. Nevertheless, they are shorter than in the parent phase CaMnO3, but longer than in CaO.
So, the present structure can be interpreted as the alternate stacking of reduced CaMnO3-type layers and of expanded CaO-type layers. The principal difference from the structure described by Fawcett et al. (1998) results in Mn polyhedra having Mn—O distances differing by ±0.03 Å from those calculated using the Shannon radii, contrasting with apical Mn—O distance of 2.09 Å with the O atom directed towards the CaO layer. This could be related to the alternate tilt of MnO6 octahedra, mainly around the x and z axes (Fig. 1a and b), of 6.8 and 8.3°, respectively, using the formulae of Elcombe et al. (1991). These tilt angles, characterized by Mn—O1—Mn 166.5 (1), Mn—O2—Mn 158.9 (2) and Mn—O3—Mn 162.5 (2)°, are quite compatible with the corresponding angles in CaMnO3.
Simulations of X-ray diffraction powder patterns with JANA2000 (Fig. 2) in both models show very small differences. This outlines, in the present case, the difficulty of refining the structure with standard X-ray powder diffraction patterns.