A novel In₃O₁₆ fragment in Cs₃In₃(PO₄)₄

The double phosphate Cs₃In₃(PO₄)₄, prepared by a flux technique, features a fragment of composition In₃O₁₆ formed by three corner-sharing InO₆ polyhedra. The central In atom resides on a twofold rotation axis, while the other two In atoms are on general positions. The O atoms in this fragment also belong to PO₄ tetra­hedra, which link the structure into an overall three-dimensional anionic In-O-P network that is penetrated by tunnels running along c. Two independent Cs⁺ cations reside inside the tunnels, one of which sits on a centre of inversion. In general, the organization of the framework is similar to that of K₃In₃(PO₄)₄, which also contains an In₃O₁₆ fragment. However, in the latter case the unit consists of one InO₇ polyhedron and one InO₆ polyhedron sharing an edge, with a third InO₆ octa­hedron connected via a shared corner. 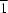Calculations of the Voronoi-Dirichlet polyhedra of the alkali metals give coordination schemes for Cs of [9+2] and [8+4] ( symmetry), and for K of [8+1], [7+2] and [7+2]. This structural analysis shows that the coordination requirements of the alkali metals residing inside the tunnels cause the difference in the In₃O₁₆ geometry.

Computing details

Data collection: CrysAlis PRO (Oxford Diffraction, 2009); cell refinement: CrysAlis PRO (Oxford Diffraction, 2009); data reduction: CrysAlis PRO (Oxford Diffraction, 2009); program(s) used to solve structure: SHELXS97 (Sheldrick, 2008); program(s) used to refine structure: SHELXL97 (Sheldrick, 2008); molecular graphics: DIAMOND (Brandenburg & Berndt, 1999); software used to prepare material for publication: WinGX (Farrugia, 1999).

tricaesium triindium tetraphosphate

Crystal data

Cs3In3(PO4)4	F(000) = 2000
Mr = 1123.07	Dx = 4.541 Mg m^−3
Monoclinic, C2/c	Mo Kα radiation, λ = 0.71073 Å
Hall symbol: -C 2yc	Cell parameters from 16601 reflections
a = 16.4370 (2) Å	θ = 2.9–41.0°
b = 10.0498 (1) Å	µ = 11.20 mm^−1
c = 9.9473 (1) Å	T = 293 K
β = 91.485 (1)°	Prism, colourless
V = 1642.63 (3) Å^3	0.20 × 0.10 × 0.01 mm
Z = 4

Data collection

Goniometer Kuma KM4/Oxford Xcalibur, detector Oxford Sapphire3 diffractometer	5338 independent reflections
Radiation source: fine-focus sealed tube	4413 reflections with I > 2σ(I)
Graphite monochromator	Rint = 0.061
Detector resolution: 16.1827 pixels mm^-1	θmax = 41.1°, θmin = 3.1°
ω and φ scans	h = −29→30
Absorption correction: multi-scan (Blessing, 1995)	k = −18→18
Tmin = 0.213, Tmax = 0.896	l = −18→18
27935 measured reflections

Refinement

Refinement on F^2	Primary atom site location: structure-invariant direct methods
Least-squares matrix: full	Secondary atom site location: difference Fourier map
R[F^2 > 2σ(F^2)] = 0.030	w = 1/[σ^2(Fo^2) + (0.0386P)^2] where P = (Fo^2 + 2Fc^2)/3
wR(F^2) = 0.070	(Δ/σ)max = 0.001
S = 1.04	Δρmax = 2.77 e Å^−3
5338 reflections	Δρmin = −2.75 e Å^−3
121 parameters	Extinction correction: SHELXL97 (Sheldrick, 2008)
0 restraints	Extinction coefficient: 0.00171 (5)

Special details

Geometry. All esds (except the esd in the dihedral angle between two l.s. planes) are estimated using the full covariance matrix. The cell esds are taken into account individually in the estimation of esds in distances, angles and torsion angles; correlations between esds in cell parameters are only used when they are defined by crystal symmetry. An approximate (isotropic) treatment of cell esds is used for estimating esds involving l.s. planes.

Refinement. Refinement of F² against ALL reflections. The weighted R-factor wR and goodness of fit S are based on F², conventional R-factors R are based on F, with F set to zero for negative F². The threshold expression of F² > σ(F²) is used only for calculating R-factors(gt) etc. and is not relevant to the choice of reflections for refinement. R-factors based on F² are statistically about twice as large as those based on F, and R- factors based on ALL data will be even larger.

Fractional atomic coordinates and isotropic or equivalent isotropic displacement parameters (Ų)

	x	y	z	Uiso*/Ueq
In1	0	0.083779 (17)	0.75	0.00754 (3)
In2	0.146950 (7)	0.181510 (12)	0.330465 (12)	0.00814 (2)
Cs1	0.112225 (10)	0.443900 (17)	0.685605 (19)	0.02624 (3)
Cs2	0.25	0.25	0	0.03236 (5)
P1	0.01047 (3)	0.21533 (5)	1.06136 (5)	0.00772 (7)
P2	0.19943 (3)	0.08388 (5)	0.64501 (5)	0.00782 (7)
O1	0.08536 (9)	0.25042 (16)	1.14726 (15)	0.0133 (3)
O2	−0.02972 (8)	0.08288 (14)	1.11447 (14)	0.0100 (2)
O3	0.03625 (9)	0.20895 (16)	0.91492 (15)	0.0133 (3)
O4	−0.05995 (9)	0.31631 (14)	1.07579 (16)	0.0126 (2)
O5	0.21365 (10)	−0.05580 (15)	0.70291 (16)	0.0141 (3)
O6	0.20687 (10)	0.08089 (17)	0.49120 (16)	0.0158 (3)
O7	0.26633 (10)	0.17355 (16)	0.70490 (17)	0.0168 (3)
O8	0.11668 (9)	0.13462 (18)	0.68684 (18)	0.0171 (3)

Atomic displacement parameters (Ų)

	U^11	U^22	U^33	U^12	U^13	U^23
In1	0.00733 (5)	0.00768 (6)	0.00759 (6)	0	0.00000 (5)	0
In2	0.00714 (4)	0.00940 (4)	0.00787 (4)	−0.00084 (3)	0.00006 (3)	−0.00003 (3)
Cs1	0.02532 (6)	0.01944 (6)	0.03344 (8)	−0.00252 (5)	−0.00935 (6)	−0.00558 (6)
Cs2	0.05061 (13)	0.02570 (10)	0.02180 (9)	0.00504 (10)	0.02102 (9)	0.00841 (8)
P1	0.00733 (14)	0.00904 (16)	0.00675 (16)	−0.00041 (13)	−0.00036 (13)	0.00028 (13)
P2	0.00682 (14)	0.00909 (16)	0.00757 (17)	−0.00131 (13)	0.00023 (13)	0.00058 (13)
O1	0.0115 (5)	0.0171 (6)	0.0112 (6)	−0.0027 (5)	−0.0032 (4)	0.0014 (5)
O2	0.0101 (4)	0.0090 (5)	0.0108 (5)	−0.0009 (4)	0.0002 (4)	0.0020 (4)
O3	0.0153 (5)	0.0167 (6)	0.0079 (5)	−0.0050 (5)	0.0012 (4)	−0.0011 (4)
O4	0.0110 (5)	0.0110 (5)	0.0159 (6)	0.0022 (4)	0.0013 (5)	0.0026 (4)
O5	0.0190 (6)	0.0107 (5)	0.0128 (6)	−0.0016 (5)	0.0018 (5)	0.0034 (4)
O6	0.0174 (6)	0.0214 (7)	0.0085 (5)	0.0032 (5)	0.0004 (5)	0.0025 (5)
O7	0.0151 (5)	0.0172 (6)	0.0179 (7)	−0.0094 (5)	−0.0014 (5)	−0.0003 (5)
O8	0.0095 (5)	0.0208 (7)	0.0212 (7)	0.0017 (5)	0.0055 (5)	0.0002 (6)

Geometric parameters (Å, º)

In1—O8	2.0968 (14)	Cs2—O3^iv	3.6161 (15)
In1—O8^i	2.0968 (14)	Cs2—O3^v	3.6161 (15)
In1—O3	2.1396 (15)	Cs2—O8^v	3.937 (2)
In1—O3^i	2.1396 (15)	Cs2—O8^v	3.937 (2)
In1—O2^ii	2.1971 (14)	P1—O1	1.5216 (15)
In1—O2^iii	2.1971 (14)	P1—O3	1.5290 (15)
In2—O7^iv	2.0744 (15)	P1—O4	1.5488 (15)
In2—O6	2.1136 (16)	P1—O2	1.5828 (14)
In2—O5^ii	2.1166 (15)	P2—O8	1.5207 (15)
In2—O1^v	2.1748 (15)	P2—O7	1.5305 (16)
In2—O4^i	2.1953 (14)	P2—O5	1.5329 (16)
In2—O2^i	2.2473 (14)	P2—O6	1.5384 (16)
Cs1—O4^i	3.0046 (16)	O1—In2^x	2.1748 (15)
Cs1—O5^vi	3.0426 (16)	O1—Cs2^x	3.1104 (15)
Cs1—O8	3.1090 (18)	O1—Cs1^xi	3.1256 (16)
Cs1—O1^vii	3.1256 (16)	O2—In1^iii	2.1971 (14)
Cs1—O7^vi	3.2225 (17)	O2—In2^i	2.2473 (14)
Cs1—O6^iv	3.5025 (16)	O3—Cs1^i	3.5220 (16)
Cs1—O4^viii	3.5050 (15)	O3—Cs2^x	3.6161 (15)
Cs1—O3^i	3.5220 (16)	O4—In2^i	2.1953 (14)
Cs1—O3	3.5334 (15)	O4—Cs1^i	3.0046 (16)
Cs1—O7	3.7162 (17)	O4—Cs1^viii	3.5050 (15)
Cs1—O4^vii	3.854 (2)	O5—In2^xii	2.1166 (15)
Cs2—O5^ii	2.8814 (16)	O5—Cs2^xiii	2.8814 (16)
Cs2—O5^ix	2.8814 (16)	O5—Cs1^xiv	3.0426 (16)
Cs2—O7^iv	3.0529 (17)	O6—Cs2^xiii	3.4008 (17)
Cs2—O7^v	3.0529 (17)	O6—Cs1^iv	3.5025 (16)
Cs2—O1^v	3.1104 (15)	O7—In2^iv	2.0744 (15)
Cs2—O1^iv	3.1104 (15)	O7—Cs2^x	3.0529 (17)
Cs2—O6^ii	3.4008 (17)	O7—Cs1^xiv	3.2225 (17)
Cs2—O6^ix	3.4008 (17)
O8—In1—O8^i	151.79 (10)	O7^iv—Cs2—O1^iv	123.54 (4)
O8—In1—O3	81.24 (6)	O7^v—Cs2—O1^iv	56.46 (4)
O8^i—In1—O3	82.28 (6)	O1^v—Cs2—O1^iv	180.00 (5)
O8—In1—O3^i	82.28 (6)	O5^ii—Cs2—O6^ii	46.28 (4)
O8^i—In1—O3^i	81.24 (6)	O5^ix—Cs2—O6^ii	133.72 (4)
O3—In1—O3^i	107.98 (9)	O7^iv—Cs2—O6^ii	104.32 (4)
O8—In1—O2^ii	101.09 (6)	O7^v—Cs2—O6^ii	75.68 (4)
O8^i—In1—O2^ii	100.32 (6)	O1^v—Cs2—O6^ii	80.22 (4)
O3—In1—O2^ii	166.34 (6)	O1^iv—Cs2—O6^ii	99.78 (4)
O3^i—In1—O2^ii	85.68 (6)	O5^ii—Cs2—O6^ix	133.72 (4)
O8—In1—O2^iii	100.32 (6)	O5^ix—Cs2—O6^ix	46.28 (4)
O8^i—In1—O2^iii	101.09 (6)	O7^iv—Cs2—O6^ix	75.68 (4)
O3—In1—O2^iii	85.68 (6)	O7^v—Cs2—O6^ix	104.32 (4)
O3^i—In1—O2^iii	166.34 (6)	O1^v—Cs2—O6^ix	99.78 (4)
O2^ii—In1—O2^iii	80.66 (8)	O1^iv—Cs2—O6^ix	80.22 (4)
O8—In1—Cs1	47.36 (5)	O6^ii—Cs2—O6^ix	180.000 (12)
O8^i—In1—Cs1	104.43 (5)	O5^ii—Cs2—O3^iv	97.54 (4)
O3—In1—Cs1	59.06 (4)	O5^ix—Cs2—O3^iv	82.46 (4)
O3^i—In1—Cs1	58.75 (4)	O7^iv—Cs2—O3^iv	81.68 (4)
O2^ii—In1—Cs1	131.88 (4)	O7^v—Cs2—O3^iv	98.32 (4)
O2^iii—In1—Cs1	132.20 (4)	O1^v—Cs2—O3^iv	137.86 (4)
O8—In1—Cs1^i	104.43 (5)	O1^iv—Cs2—O3^iv	42.14 (4)
O8^i—In1—Cs1^i	47.36 (5)	O6^ii—Cs2—O3^iv	108.55 (4)
O3—In1—Cs1^i	58.75 (4)	O6^ix—Cs2—O3^iv	71.45 (4)
O3^i—In1—Cs1^i	59.06 (4)	O5^ii—Cs2—O3^v	82.46 (4)
O2^ii—In1—Cs1^i	132.20 (4)	O5^ix—Cs2—O3^v	97.54 (4)
O2^iii—In1—Cs1^i	131.88 (4)	O7^iv—Cs2—O3^v	98.32 (4)
Cs1—In1—Cs1^i	57.080 (5)	O7^v—Cs2—O3^v	81.68 (4)
O7^iv—In2—O6	98.94 (7)	O1^v—Cs2—O3^v	42.14 (4)
O7^iv—In2—O5^ii	87.06 (6)	O1^iv—Cs2—O3^v	137.86 (4)
O6—In2—O5^ii	85.95 (6)	O6^ii—Cs2—O3^v	71.45 (4)
O7^iv—In2—O1^v	86.63 (6)	O6^ix—Cs2—O3^v	108.55 (4)
O6—In2—O1^v	169.70 (6)	O3^iv—Cs2—O3^v	180.000 (12)
O5^ii—In2—O1^v	85.69 (6)	O5^ii—Cs2—P2^ii	22.09 (3)
O7^iv—In2—O4^i	95.55 (6)	O5^ix—Cs2—P2^ii	157.91 (3)
O6—In2—O4^i	105.66 (6)	O7^iv—Cs2—P2^ii	80.19 (3)
O5^ii—In2—O4^i	167.48 (6)	O7^v—Cs2—P2^ii	99.81 (3)
O1^v—In2—O4^i	82.26 (6)	O1^v—Cs2—P2^ii	67.43 (3)
O7^iv—In2—O2^i	161.50 (6)	O1^iv—Cs2—P2^ii	112.57 (3)
O6—In2—O2^i	89.45 (6)	O6^ii—Cs2—P2^ii	24.19 (3)
O5^ii—In2—O2^i	110.09 (6)	O6^ix—Cs2—P2^ii	155.81 (3)
O1^v—In2—O2^i	87.78 (5)	O3^iv—Cs2—P2^ii	103.62 (3)
O4^i—In2—O2^i	66.20 (5)	O3^v—Cs2—P2^ii	76.38 (3)
O7^iv—In2—P1^i	127.97 (5)	O5^ii—Cs2—P2^ix	157.91 (3)
O6—In2—P1^i	100.45 (4)	O5^ix—Cs2—P2^ix	22.09 (3)
O5^ii—In2—P1^i	141.94 (4)	O7^iv—Cs2—P2^ix	99.81 (3)
O1^v—In2—P1^i	82.58 (4)	O7^v—Cs2—P2^ix	80.19 (3)
O4^i—In2—P1^i	32.62 (4)	O1^v—Cs2—P2^ix	112.57 (3)
O2^i—In2—P1^i	33.64 (4)	O1^iv—Cs2—P2^ix	67.43 (3)
O7^iv—In2—Cs2	53.30 (5)	O6^ii—Cs2—P2^ix	155.81 (3)
O6—In2—Cs2	122.12 (4)	O6^ix—Cs2—P2^ix	24.19 (3)
O5^ii—In2—Cs2	48.71 (4)	O3^iv—Cs2—P2^ix	76.38 (3)
O1^v—In2—Cs2	54.95 (4)	O3^v—Cs2—P2^ix	103.62 (3)
O4^i—In2—Cs2	124.45 (4)	P2^ii—Cs2—P2^ix	180.000 (6)
O2^i—In2—Cs2	134.03 (4)	O1—P1—O3	107.74 (8)
P1^i—In2—Cs2	137.300 (10)	O1—P1—O4	113.07 (9)
O7^iv—In2—Cs1^vii	51.72 (5)	O3—P1—O4	110.00 (9)
O6—In2—Cs1^vii	140.30 (5)	O1—P1—O2	110.24 (8)
O5^ii—In2—Cs1^vii	114.23 (4)	O3—P1—O2	114.27 (8)
O1^v—In2—Cs1^vii	49.47 (4)	O4—P1—O2	101.58 (8)
O4^i—In2—Cs1^vii	59.48 (4)	O1—P1—In2^i	123.03 (6)
O2^i—In2—Cs1^vii	112.42 (4)	O3—P1—In2^i	129.19 (6)
P1^i—In2—Cs1^vii	84.424 (10)	O4—P1—In2^i	49.82 (6)
Cs2—In2—Cs1^vii	65.625 (3)	O2—P1—In2^i	51.87 (5)
O7^iv—In2—Cs1^iv	63.11 (5)	O1—P1—Cs1^i	128.07 (6)
O6—In2—Cs1^iv	57.25 (4)	O3—P1—Cs1^i	64.84 (6)
O5^ii—In2—Cs1^iv	44.62 (4)	O4—P1—Cs1^i	45.16 (6)
O1^v—In2—Cs1^iv	119.13 (4)	O2—P1—Cs1^i	119.57 (5)
O4^i—In2—Cs1^iv	146.52 (4)	In2^i—P1—Cs1^i	81.246 (11)
O2^i—In2—Cs1^iv	134.29 (4)	O1—P1—Cs1^xi	45.67 (6)
P1^i—In2—Cs1^iv	157.673 (11)	O3—P1—Cs1^xi	101.93 (6)
Cs2—In2—Cs1^iv	64.900 (3)	O4—P1—Cs1^xi	73.58 (6)
Cs1^vii—In2—Cs1^iv	113.064 (4)	O2—P1—Cs1^xi	142.47 (6)
O7^iv—In2—Cs1	79.72 (5)	In2^i—P1—Cs1^xi	111.268 (14)
O6—In2—Cs1	75.54 (5)	Cs1^i—P1—Cs1^xi	83.981 (10)
O5^ii—In2—Cs1	155.13 (4)	O1—P1—Cs2^x	44.20 (6)
O1^v—In2—Cs1	114.17 (4)	O3—P1—Cs2^x	64.00 (6)
O4^i—In2—Cs1	36.86 (4)	O4—P1—Cs2^x	134.06 (6)
O2^i—In2—Cs1	86.53 (4)	O2—P1—Cs2^x	122.89 (5)
P1^i—In2—Cs1	59.582 (10)	In2^i—P1—Cs2^x	166.362 (17)
Cs2—In2—Cs1	130.367 (4)	Cs1^i—P1—Cs2^x	110.320 (11)
Cs1^vii—In2—Cs1	73.346 (3)	Cs1^xi—P1—Cs2^x	64.413 (7)
Cs1^iv—In2—Cs1	110.557 (4)	O8—P2—O7	109.56 (10)
O4^i—Cs1—O5^vi	124.13 (4)	O8—P2—O5	109.45 (9)
O4^i—Cs1—O8	65.35 (4)	O7—P2—O5	106.97 (9)
O5^vi—Cs1—O8	88.72 (4)	O8—P2—O6	111.93 (9)
O4^i—Cs1—O1^vii	106.11 (4)	O7—P2—O6	108.89 (10)
O5^vi—Cs1—O1^vii	99.91 (4)	O5—P2—O6	109.91 (9)
O8—Cs1—O1^vii	170.51 (4)	O8—P2—Cs2^xiii	127.84 (7)
O4^i—Cs1—O7^vi	139.37 (4)	O7—P2—Cs2^xiii	120.78 (7)
O5^vi—Cs1—O7^vi	46.17 (4)	O5—P2—Cs2^xiii	44.99 (6)
O8—Cs1—O7^vi	134.45 (4)	O6—P2—Cs2^xiii	64.93 (7)
O1^vii—Cs1—O7^vi	54.66 (4)	O8—P2—Cs1^xiv	137.30 (7)
O4^i—Cs1—O6^iv	76.27 (4)	O7—P2—Cs1^xiv	58.05 (7)
O5^vi—Cs1—O6^iv	51.70 (4)	O5—P2—Cs1^xiv	51.18 (6)
O8—Cs1—O6^iv	84.87 (4)	O6—P2—Cs1^xiv	110.65 (6)
O1^vii—Cs1—O6^iv	97.34 (4)	Cs2^xiii—P2—Cs1^xiv	69.497 (9)
O7^vi—Cs1—O6^iv	72.19 (4)	O8—P2—Cs1	47.91 (7)
O4^i—Cs1—O4^viii	144.08 (5)	O7—P2—Cs1	71.16 (7)
O5^vi—Cs1—O4^viii	89.85 (4)	O5—P2—Cs1	149.30 (6)
O8—Cs1—O4^viii	133.70 (4)	O6—P2—Cs1	99.17 (7)
O1^vii—Cs1—O4^viii	50.99 (4)	Cs2^xiii—P2—Cs1	161.923 (14)
O7^vi—Cs1—O4^viii	55.90 (4)	Cs1^xiv—P2—Cs1	126.788 (13)
O6^iv—Cs1—O4^viii	127.96 (4)	O8—P2—Cs2^x	77.53 (7)
O4^i—Cs1—O3^i	44.58 (4)	O7—P2—Cs2^x	43.55 (7)
O5^vi—Cs1—O3^i	137.95 (4)	O5—P2—Cs2^x	91.40 (6)
O8—Cs1—O3^i	49.23 (4)	O6—P2—Cs2^x	150.66 (7)
O1^vii—Cs1—O3^i	121.98 (4)	Cs2^xiii—P2—Cs2^x	132.342 (13)
O7^vi—Cs1—O3^i	174.09 (4)	Cs1^xiv—P2—Cs2^x	66.928 (8)
O6^iv—Cs1—O3^i	113.63 (4)	Cs1—P2—Cs2^x	65.733 (8)
O4^viii—Cs1—O3^i	118.23 (3)	P1—O1—In2^x	138.51 (9)
O4^i—Cs1—O3	100.11 (4)	P1—O1—Cs2^x	115.87 (8)
O5^vi—Cs1—O3	96.33 (4)	In2^x—O1—Cs2^x	90.14 (5)
O8—Cs1—O3	48.55 (4)	P1—O1—Cs1^xi	113.95 (8)
O1^vii—Cs1—O3	133.19 (4)	In2^x—O1—Cs1^xi	98.60 (5)
O7^vi—Cs1—O3	119.12 (4)	Cs2^x—O1—Cs1^xi	86.38 (4)
O6^iv—Cs1—O3	126.54 (4)	P1—O2—In1^iii	139.27 (8)
O4^viii—Cs1—O3	85.72 (3)	P1—O2—In2^i	94.49 (7)
O3^i—Cs1—O3	58.76 (5)	In1^iii—O2—In2^i	111.41 (6)
O4^i—Cs1—O7	84.95 (4)	P1—O3—In1	132.58 (9)
O5^vi—Cs1—O7	49.34 (4)	P1—O3—Cs1^i	92.02 (7)
O8—Cs1—O7	41.66 (4)	In1—O3—Cs1^i	89.96 (5)
O1^vii—Cs1—O7	144.97 (4)	P1—O3—Cs1	134.29 (8)
O7^vi—Cs1—O7	95.206 (9)	In1—O3—Cs1	89.66 (5)
O6^iv—Cs1—O7	52.23 (4)	Cs1^i—O3—Cs1	67.83 (3)
O4^viii—Cs1—O7	130.27 (4)	P1—O3—Cs2^x	93.66 (6)
O3^i—Cs1—O7	89.48 (3)	In1—O3—Cs2^x	119.74 (6)
O3—Cs1—O7	74.33 (4)	Cs1^i—O3—Cs2^x	130.68 (4)
O4^i—Cs1—P2^vi	139.58 (3)	Cs1—O3—Cs2^x	73.58 (3)
O5^vi—Cs1—P2^vi	23.11 (3)	P1—O4—In2^i	97.56 (7)
O8—Cs1—P2^vi	110.69 (3)	P1—O4—Cs1^i	113.40 (8)
O1^vii—Cs1—P2^vi	78.40 (3)	In2^i—O4—Cs1^i	117.14 (6)
O7^vi—Cs1—P2^vi	23.76 (3)	P1—O4—Cs1^viii	135.25 (8)
O6^iv—Cs1—P2^vi	63.36 (3)	In2^i—O4—Cs1^viii	87.87 (5)
O4^viii—Cs1—P2^vi	69.68 (2)	Cs1^i—O4—Cs1^viii	102.88 (4)
O3^i—Cs1—P2^vi	159.17 (3)	P2—O5—In2^xii	134.07 (9)
O3—Cs1—P2^vi	105.16 (3)	P2—O5—Cs2^xiii	112.92 (8)
O7—Cs1—P2^vi	72.43 (3)	In2^xii—O5—Cs2^xiii	97.80 (5)
O4^i—Cs1—P1^i	21.44 (3)	P2—O5—Cs1^xiv	105.70 (7)
O5^vi—Cs1—P1^i	134.30 (3)	In2^xii—O5—Cs1^xiv	106.13 (6)
O8—Cs1—P1^i	54.81 (3)	Cs2^xiii—O5—Cs1^xiv	92.55 (4)
O1^vii—Cs1—P1^i	115.73 (3)	P2—O6—In2	134.06 (10)
O7^vi—Cs1—P1^i	160.59 (3)	P2—O6—Cs2^xiii	90.88 (7)
O6^iv—Cs1—P1^i	94.24 (3)	In2—O6—Cs2^xiii	125.45 (7)
O4^viii—Cs1—P1^i	134.56 (2)	P2—O6—Cs1^iv	126.25 (8)
O3^i—Cs1—P1^i	23.14 (2)	In2—O6—Cs1^iv	92.25 (5)
O3—Cs1—P1^i	80.03 (3)	Cs2^xiii—O6—Cs1^iv	76.37 (3)
O7—Cs1—P1^i	86.70 (3)	P2—O7—In2^iv	146.87 (11)
P2^vi—Cs1—P1^i	155.754 (11)	P2—O7—Cs2^x	116.25 (8)
O5^ii—Cs2—O5^ix	180.00 (4)	In2^iv—O7—Cs2^x	93.69 (6)
O5^ii—Cs2—O7^iv	58.12 (4)	P2—O7—Cs1^xiv	98.19 (8)
O5^ix—Cs2—O7^iv	121.88 (4)	In2^iv—O7—Cs1^xiv	97.93 (6)
O5^ii—Cs2—O7^v	121.88 (4)	Cs2^x—O7—Cs1^xiv	85.66 (4)
O5^ix—Cs2—O7^v	58.12 (4)	P2—O7—Cs1	85.89 (7)
O7^iv—Cs2—O7^v	180.000 (17)	In2^iv—O7—Cs1	87.04 (5)
O5^ii—Cs2—O1^v	58.15 (4)	Cs2^x—O7—Cs1	77.81 (4)
O5^ix—Cs2—O1^v	121.85 (4)	Cs1^xiv—O7—Cs1	163.04 (6)
O7^iv—Cs2—O1^v	56.46 (4)	P2—O8—In1	146.28 (11)
O7^v—Cs2—O1^v	123.54 (4)	P2—O8—Cs1	110.81 (8)
O5^ii—Cs2—O1^iv	121.85 (4)	In1—O8—Cs1	102.90 (6)
O5^ix—Cs2—O1^iv	58.15 (4)

Symmetry codes: (i) −x, y, −z+3/2; (ii) x, −y, z−1/2; (iii) −x, −y, −z+2; (iv) −x+1/2, −y+1/2, −z+1; (v) x, y, z−1; (vi) −x+1/2, y+1/2, −z+3/2; (vii) x, −y+1, z−1/2; (viii) −x, −y+1, −z+2; (ix) −x+1/2, y+1/2, −z+1/2; (x) x, y, z+1; (xi) x, −y+1, z+1/2; (xii) x, −y, z+1/2; (xiii) −x+1/2, y−1/2, −z+1/2; (xiv) −x+1/2, y−1/2, −z+3/2.