Buy article online - an online subscription or single-article purchase is required to access this article.
A periodic lattice in 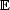 n is associated with an n-grid and its dual, and with a point symmetry group G. Given a subgroup H of G, a subspace
n is associated with an n-grid and its dual, and with a point symmetry group G. Given a subgroup H of G, a subspace 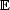 m, m < n, of
m, m < n, of 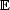 n, invariant under H, is chosen and a projection of the n-grid from
n, invariant under H, is chosen and a projection of the n-grid from 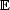 n to
n to 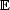 m is defined. The translational and point symmetries of the projected n-grid are analyzed. A projection of the cubic n-grid from
m is defined. The translational and point symmetries of the projected n-grid are analyzed. A projection of the cubic n-grid from 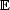 n to
n to 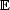 n-1 based on H = S(n) yields a periodic n-grid. A projection of the cubic 12-grid from
n-1 based on H = S(n) yields a periodic n-grid. A projection of the cubic 12-grid from 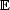 12 to
12 to 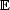 3 based on H = A(5) yields a non-periodic 12-grid. This 12- grid is characterized by three real numbers and from its projection has a well defined orientation. The dual to this 12-grid yields a generalization of the non-periodic Penrose patterns from two to three dimensions.
3 based on H = A(5) yields a non-periodic 12-grid. This 12- grid is characterized by three real numbers and from its projection has a well defined orientation. The dual to this 12-grid yields a generalization of the non-periodic Penrose patterns from two to three dimensions.

 journal menu
journal menu









 Subscribe to Acta Crystallographica Section A: Foundations and Advances
Subscribe to Acta Crystallographica Section A: Foundations and Advances


