On the entropy to texture index relationship in quantitative texture analysis

This communication demonstrates a sharp inequality between the 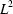-norm and the entropy of probability density functions. This inequality is applied to texture analysis, and the relationship between the entropy and the texture index of an orientation density function is characterized. More precisely, the orientation space is shown to allow for texture index and entropy variations of orientation probability density functions between an upper and a lower bound for the entropy. In this way, it is proved that there is no functional relationship between entropy and texture index of an orientation probability density function as conjectured previously on the basis of practical numerical texture analyses using the widely used pole-to-orientation probability density function reconstruction software WIMV, known by the initials of its authors and their ancestors (Williams-Imhof-Matthies-Vinel). Synthetic orientation probability density functions were then synthesized, covering a large domain of variation for texture index and entropy, and used to check the numerical results of the same software package.