Buy article online - an online subscription or single-article purchase is required to access this article.
Methods are presented for an analysis of zones and sublattices of integral lattices, whose relevance is revealed by sharp peaks in the frequency distribution of hexagonal and tetragonal lattices, as a function of the axial ratio 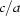 . Starting from a few examples, zone symmetries, lattice-sublattice relations and integral scaling transformations are derived for hexagonal lattices with axial ratios
. Starting from a few examples, zone symmetries, lattice-sublattice relations and integral scaling transformations are derived for hexagonal lattices with axial ratios 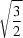 ,
, 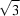 ,
, 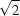 and 1 (the isometric case) and for the related
and 1 (the isometric case) and for the related 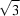 and
and 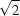 tetragonal lattices. Sublattices and zones connected by linear rational transformations lead to rational equivalence classes of integral lattices. For properties like the axial ratio and the point-group symmetry (lattice holohedry), rational equivalence can be extended so that also metric tensors differing by an integral factor become equivalent. These two types of equivalence classes are determined for the lattices mentioned above.
tetragonal lattices. Sublattices and zones connected by linear rational transformations lead to rational equivalence classes of integral lattices. For properties like the axial ratio and the point-group symmetry (lattice holohedry), rational equivalence can be extended so that also metric tensors differing by an integral factor become equivalent. These two types of equivalence classes are determined for the lattices mentioned above.

 journal menu
journal menu









 Subscribe to Acta Crystallographica Section A: Foundations and Advances
Subscribe to Acta Crystallographica Section A: Foundations and Advances


