1,3,5-Triphenyl­adamantane and 1,3,5,7-tetra­phenyl­adamantane

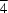
In 1,3,5-triphenyl­adamantane, C₂₈H₂₈, (I), and 1,3,5,7-tetra­phenyl­adamantane, C₃₄H₃₂, (II), the mol­ecules possess symmetries 3 and , and are situated across threefold and fourfold improper axes, respectively. The mol­ecules aggregate by means of extensive C-H...[pi] inter­actions. In (I), the pyramidal shape of the mol­ecules dicta­tes the formation of dimers through a `sixfold phenyl embrace' pattern. The dimers are linked to six close neighbors and constitute a primitive cubic net [H...[pi] = 2.95 (2) and 3.02 (2) Å]. Compound (II) is isomorphous with tetra­phenyl derivatives EPh₄ of group 14 (E = C-Pb) and ionic salts [EPh₄][BPh₄] (E = P, As and Sb). The multiple C-H...[pi] inter­actions arrange the mol­ecules into chains, with a concerted action of CH (phen­yl) and CH₂ (adamantane) groups as donors [H...[pi] = 3.15 (2) and 3.44 (2) Å, respectively]. The additional inter­actions with the methyl­ene groups (four per mol­ecule) are presumably important for explaining the high melting point and insolubility of (II) compared with the EPh₄ analogs.

S1. Comment

Derivatives of adamantane attract a broad interdisciplinary interest as rigid molecular scaffolds for sustaining the structures of polyfunctional species, which find various applications in the chemistry of supramolecular systems, macromolecules, dendrimers and polymers. Thus adamantanes substituted in the four available bridgehead positions represent a family of rigid tetrahedral building blocks for the synthesis of hydrogen- and coordination-bonded framework polymers, and they are paradigmatic for the general principles of crystal design. In particular, the fivefold-interpenetrated diamondoid framework of 1,3,5,7-adamantanetetracarboxylate (Ermer, 1988) was of paramount significance for the development of crystal engineering and for stimulating many further efforts in this field (Moulton & Zaworotko, 2001).

In recent years, considerable attention has been focused on the synthesis and utilization of nanosized adamantane derivatives extended by a rigid 1,4-phenylene spacer (Reichert & Mathias, 1994). Following this methodology, such species as carboxylates (Kim et al., 2001), phosphonates (Jones et al., 2006) and sulfonates (Hoffart et al., 2005) were accessible by functionalization of phenyl-substituted adamantanes. However, supramolecular relations in such systems may be complicated, and close alignment of large shape-complementary tectons of high molecular symmetry could be prevalent for the crystal packing. This mitigates against the preparation of very open structures and makes the synthesis more difficult owing to the very poor solubility of the organic tectons. When exploring the evident potential of the extended adamantanes for the development of framework solids (Chen et al., 2000), the structures of the simpler phenyl derivatives are particularly interesting. The latter may be considered as prototypal building blocks, which assemble into framework structures through C—H···π interactions between the multiple phenyl functions (Nishio et al., 1998). These interactions clearly define the elegant structure of 1,3-diphenyladamantane, which contains supramolecular helices (Tukada & Mochizuki, 2003). Even more illustrative supramolecular relations may be anticipated for rigid tri- and tetrasubstituted molecules since multivalency of the building blocks and inherently defined and proper binding geometry are equally important factors for organization of the framework. Concerted C—H···π interactions are presumably responsible for the unusual properties of a tetraphenyl derivative, which is an exceptionally high-melting (melting point 690–692 K) and insoluble solid (Newman, 1972). We have examined polyfunctional 1,3,5-triphenyladamantane, (I), and 1,3,5,7-tetraphenyladamantane, (II), and report their structures here.

Molecules of (I) have 3 symmetry in the crystalline state, with the C4/H4 group lying on a threefold axis (Fig. 1), and therefore there is only one independent phenyl group. It adopts a nearly eclipsed conformation to one of the C—C bonds of the adamantane carrier [e.g. C2ⁱ—C1—C5—C6 = -6.71 (16)°; symmetry code: (i) -x + y, -x + 1, z; see also Table 1], similar to the conformation in 1,3-diphenyladamantane (Tukada & Mochizuki, 2003).

The most peculiar feature of the crystal packing of (I) is a pair-wise association of the molecules, leading to the formation of a tight `supramolecular cube' (Fig. 2). The dimer possesses 3 symmetry and it is supported by very characteristic C—H···π interactions between the six phenyl rings. Each pair of interacting rings adopts an interplanar angle of 73.55 (4)°. These weak interactions are directional and the H atom is situated almost exactly above the neighboring ring centroid [symmetry code: (iii) y - 1/3, -x + y+1/3, -z + 1/3], with an angle of the H···π axis to the plane of the aromatic ring of 83.1 (10)° (Table 2). Such a mode of shape-complementary association, often recognized as a `sixfold phenyl embrace', is characteristic for pyramidal triphenyl-substituted molecules, and it was observed for several triphenylphosphines (Scudder & Dance 2000), triphenylgermanium halogenides (Prince et al., 2002) and even for charged species, such as triphenyltelluronium cations (Närhi et al., 2004). A distance of 6.136 (2) Å between the centroids of adamantane frameworks indicates very tight coupling of the molecules constituting the dimer.

One additional group, C10/H10, is involved in an interdimer C—H···π interaction, which is comparable in strength to that above, with an H···π^vi separation of 2.95 (2) Å [symmetry code: (vi) y, -x + y, -z; Fig. 3]. In total, six phenyl groups of the dimer provide connections to six closest neighbors. Thus the entire structure is very simple, and it may be regarded as a primitive cubic lattice with the supramolecular dimers as the net points. Alternatively, the structure may be described as a three-dimensional C—H···π phenyl stack of NbO topology, with bulky adamantane groups populating the framework cages.

Molecules of (II) have 4 symmetry in the crystal; they are situated on the improper fourfold axis passing through atoms C2 and C2ⁱ [symmetry code: (i) y, -x, z; Fig. 4], and display the expected tetrahedral geometry (Table 3) with the following angles subtended by the Cg—Ph vectors [Cg is the centroid of the adamantane group at (0,0,0)]: C4—Cg—C4ⁱⁱ = 106.74 (6)° and C4—Cg—C4ⁱⁱⁱ = 110.86 (6)° [symmetry codes: (ii) -x, -y, z; (iii) -y, x, -z].

The structure is isomorphous with a family of tetraphenyl derivatives EPh₄ of group 14 elements (E = C, Si, Ge, Sn and Pb; Claborn et al., 2002) and also with tetraphenylosmium(IV) (Stavropoulos et al., 1987). All the members of this family uniformly crystallize in the tetragonal space group P42₁c with very similar unit-cell parameters. Ionic salts of the type [EPh₄][BPh₄] (E = P, As and Sb) also adopt such a structure, while crystallizing in a supercell of P42₁c with ordered positions of the ionic counterparts (Lloyd & Brock, 1997). Thus (II) is a simple expanded analog of the above tetrahedral molecules, with a Cg···C(Ph) separation [3.1006 (16) Å] formally corresponding to the E—C bonds of EPh₄. The structure of (II) is organized by means of very extensive C—H···π interactions, leading to a packing index of 70.4. Although the value resides exactly at the mid-point of the 65–75% range expected for organic solids (Dunitz, 1995), it only slightly exceeds the parameters for the related EPh₄ structures, e.g. 69.3 for E = Si and 69.9 for E = C (Claborn et al., 2002). In this context, it is interesting to query why these materials are so different in view of their properties, since (II) possesses an exceptionally low solubility in all common solvents and also an incomparably high melting point.

The primary supramolecular pattern is a one-dimensional chain, running along the c axis, in which the molecules are stacked like the pieces of a puzzle, yielding concerted cycles of four edge-to-face phenyl–phenyl interactions [C5—H5···π^v = 3.15 (2) Å, symmetry code: (v) y, -x, -z + 1; Figs. 5 and 6]. In the chain, the molecules of (II) are related by translation along the c-axis direction [7.2032 (6) Å] and are packed even more closely than in tetraphenylmethane [7.287 (2) Å; Robbins et al., 1975]. The interchain bonding occurs by means of double C6/H6,C7/H7···π^vi [symmetry code: (vi) y + 1/2, x - 1/2, z + 1/2] interactions, yielding a typical herringbone arrangement of the phenyl groups (Fig. 6 and Table 4). These interactions are consistent with those in tetraphenyllead [H···π = 3.28 Å; C···π = 3.949 and 3.958 Å; Preut & Huber, 1993] and are somewhat stronger than those in tetraphenylmethane (H···π = 3.43 and 3.73 Å; C···π = 4.166 and 4.306 Å).

The set of C—H···π interactions affords a three-dimensional stack (Fig. 7) and this motif is common for all the present family. The most notable feature of the packing, which is applicable to adamantane (II) only, is a set of directional C2—H2···π^v contacts with the methylene group [H···π = 3.44 (2) Å and C—H···π = 177.6 (15)°; Fig. 5]. Such distal interactions are unlikely to be attributed to hydrogen bonding and presumably they originate in very weak dispersion forces. However, the cooperative effect of four such geometrically favored interactions per molecule of (II) may be significant (Suezawa et al., 2001). This contributes to the overall energy of the supramolecular structure as an additional force compared with the isomorphous tetraphenyl derivatives of group 14. The fact that the concerted interactions C5—H5—π^v and C2—H2—π^v facilitate the densest interaction between the molecules may be applicable for other phenyl-substituted adamantanes as a special type of `supramolecular synthon' organizing molecules in the solid state. In (I), such interactions are negated by the formation of the more prevalent `sixfold phenyl embrace' pattern and there are no close contacts with the methylene group. However, the aforementioned interactions are relevant for 1,3-diphenyladamantane [C—H···π = 3.39 Å (Ph) and 3.52 Å (CH₂); Tukada & Mochizuki, 2003], 1,3,5,7-tetrakis(4-phosphonophenyl)adamantane [C—H···π = 3.28 Å (Ph) and 3.52 Å (CH₂); Jones et al., 2006] and 1,3,5,7-tetrakis(4-ethynylphenyl)adamantane [C—H···π = 3.55 Å (Ph) and 3.52 Å (CH₂); Galoppini & Gilardi, 1999].

In brief, the title structures are important as general and basic prototypes for intermolecular interactions between extended polyaryl-substituted adamantanes, which are currently arousing growing interest as molecular scaffolds in supramolecular chemistry. A comparison of (II) and a series of isomorphous tetraphenyl-substituted molecules allows the postulation of the significance of the weakest forces, such as methylene–π interactions.

Related literature

For related literature, see: Chen et al. (2000); Claborn et al. (2002); Dunitz (1995); Ermer (1988); Galoppini & Gilardi (1999); Hoffart et al. (2005); Jones et al. (2006); Kim et al. (2001); Lloyd & Brock (1997); Moulton & Zaworotko (2001); Narhi et al. (2004); Newman (1972); Nishio et al. (1998); Preut & Huber (1993); Prince et al. (2002); Reichert & Mathias (1994); Robbins et al. (1975); Scudder & Dance (2000); Stavropoulos et al. (1987); Suezawa et al. (2001).

S2. Experimental

Compounds (I) and (II) were synthesized in a 15–20 g scale by Friedel–Crafts reaction of 1-bromoadamantane and benzene in the presence of tert-butyl bromide using procedure of Newman (1972). Crude (I) was repeatedly washed with ether to remove traces of mono- and diphenyladamantanes and then crystallized from hot toluene as large colorless prisms. Compound (II), which is insoluble in all common solvents, was purified from partially phenylated adamantanes by continuous extraction with hot toluene in a Soxhlet apparatus. For crystallization, the resulting colorless powder (15 mg) and xylene (8 ml, mixture of isomers) were sealed in a Pyrex tube and heated at 473 K for 2 d. Slow cooling to room temperature over a period of 70 h provides small colorless prisms of (II) in a quantitative yield.

S3. Refinement

For (II), the Friedel-related reflections were merged. For both structures, all the H atoms were found in intermediate difference Fourier maps and were refined fully with isotropic displacement parameters [for (I), C—H (phenyl) = 0.957 (16)–0.986 (15) Å and C—H (aliphatic) = 1.006 (14)–1.034(14) Å; for (II) C—H (phenyl) = 0.94 (2)–1.00 (2) Å and C—H (aliphatic) = 0.984 (19)–1.009 (18) Å].

Computing details

Data collection: SMART-NT (Bruker, 1998) for (I); IPDS Software (Stoe & Cie, 2000) for (II). Cell refinement: SAINT-NT (Bruker, 1999) for (I); IPDS Software (Stoe & Cie, 2000) for (II). Data reduction: SAINT-NT (Bruker, 1999) for (I); IPDS Software (Stoe & Cie, 2000) for (II). For both compounds, program(s) used to solve structure: SHELXS97 (Sheldrick, 2008); program(s) used to refine structure: SHELXL97 (Sheldrick, 2008); molecular graphics: Diamond (Brandenburg, 1999); software used to prepare material for publication: WinGX (Farrugia, 1999).

Figures

	Fig. 1. The structure of (I), showing the atom-labeling scheme. Displacement ellipsoids are drawn at the 50% probability level. The threefold axis lies along the C4—H4 direction. [Symmetry codes: (i) -x + y, -x + 1, z; (ii) -y + 1, x - y + 1, z.]
	Fig. 2. The supramolecular cube formed by two molecules of (I) by means of concerted C—H···π interactions (shown as dashed lines) of six phenyl groups. Atoms C4 and C4^v are situated on the improper threefold axis. [Symmetry codes: (iii) y - 1/3, -x + y + 1/3, -z + 1/3; (iv) x - y + 2/3, x + 1/3, -z + 1/3; (v) -x + 2/3, -y + 4/3, -z + 1/3.]
	Fig. 3. A view of the structure of (I), showing C—H···π interactions (dashed lines) between the neighboring dimeric supramolecular entities. The same connectivity occurs also in the direction which is orthogonal to the plane of the drawing. [Symmetry code: (vi) y, -x + y, -z.]
	Fig. 4. The structure of (II), showing the atom-labeling scheme. Displacement ellipsoids are drawn at the 35% probability level. The improper fourfold axis passes through atoms C2 and C2^i. [Symmetry codes: (i) y, -x, -z; (ii) -x, -y, z; (iii) -y, x, -z.]
	Fig. 5. Multiple C—H···π interactions between pairs of molecules of (II), which lead to the formation of one-dimensional chains. Note the concerted interaction employing pairs of aromatic and aliphatic CH groups. [Symmetry codes: (iv) -y, x, 1 - z; (v) y, -x, -z + 1.]
	Fig. 6. A view of the structure of (II), showing chains running along the c-axis direction. The C—H···π interactions between the chains produce a characteristic herringbone phenyl motif (which is shown with bold shaded bonds). [Symmetry codes: (v) y, -x, -z + 1; (vi) y + 1/2, x - 1/2, z + 1/2.]
	Fig. 7. Projection of the structure of (II) on to the ab plane. The dashed lines indicate C—H···π interactions.

(I) 1,3,5-Triphenyladamantane

Crystal data

C28H28	Dx = 1.248 Mg m^−3
Mr = 364.50	Mo Kα radiation, λ = 0.71073 Å
Trigonal, R3	Cell parameters from 3995 reflections
a = 13.0230 (4) Å	θ = 2.1–26.6°
c = 19.8046 (13) Å	µ = 0.07 mm^−1
V = 2908.8 (2) Å^3	T = 173 K
Z = 6	Prism, colorless
F(000) = 1176	0.24 × 0.23 × 0.16 mm

Data collection

Siemens SMART CCD area-detector diffractometer	1345 independent reflections
Radiation source: fine-focus sealed tube	1039 reflections with I > 2σ(I)
Graphite monochromator	Rint = 0.027
ω scans	θmax = 26.6°, θmin = 2.1°
Absorption correction: empirical (using intensity measurements) (SADABS; Sheldrick, 1996)	h = −16→15
Tmin = 0.978, Tmax = 0.989	k = −16→9
3995 measured reflections	l = −20→24

Refinement

Refinement on F^2	Primary atom site location: structure-invariant direct methods
Least-squares matrix: full	Secondary atom site location: difference Fourier map
R[F^2 > 2σ(F^2)] = 0.039	Hydrogen site location: difference Fourier map
wR(F^2) = 0.103	All H-atom parameters refined
S = 1.04	w = 1/[σ^2(Fo^2) + (0.0478P)^2 + 1.6227P] where P = (Fo^2 + 2Fc^2)/3
1345 reflections	(Δ/σ)max < 0.001
123 parameters	Δρmax = 0.20 e Å^−3
0 restraints	Δρmin = −0.20 e Å^−3

Special details

Geometry. All e.s.d.'s (except the e.s.d. in the dihedral angle between two l.s. planes) are estimated using the full covariance matrix. The cell e.s.d.'s are taken into account individually in the estimation of e.s.d.'s in distances, angles and torsion angles; correlations between e.s.d.'s in cell parameters are only used when they are defined by crystal symmetry. An approximate (isotropic) treatment of cell e.s.d.'s is used for estimating e.s.d.'s involving l.s. planes.

Refinement. Refinement of F² against ALL reflections. The weighted R-factor wR and goodness of fit S are based on F², conventional R-factors R are based on F, with F set to zero for negative F². The threshold expression of F² > σ(F²) is used only for calculating R-factors(gt) etc. and is not relevant to the choice of reflections for refinement. R-factors based on F² are statistically about twice as large as those based on F, and R- factors based on ALL data will be even larger.

Fractional atomic coordinates and isotropic or equivalent isotropic displacement parameters (Ų)

	x	y	z	Uiso*/Ueq
C1	0.23727 (11)	0.54185 (11)	0.03772 (6)	0.0197 (3)
C2	0.36207 (11)	0.57327 (11)	0.06270 (6)	0.0194 (3)
C3	0.23791 (12)	0.54424 (12)	−0.04037 (6)	0.0229 (3)
C4	0.3333	0.6667	−0.06534 (11)	0.0229 (5)
C5	0.14844 (11)	0.41950 (11)	0.06478 (6)	0.0204 (3)
C6	0.06223 (11)	0.40124 (12)	0.11271 (6)	0.0232 (3)
C7	−0.01017 (12)	0.28992 (12)	0.14072 (7)	0.0273 (3)
C8	0.00033 (12)	0.19410 (12)	0.12051 (7)	0.0275 (3)
C9	0.08318 (12)	0.21003 (12)	0.07195 (7)	0.0260 (3)
C10	0.15614 (12)	0.32061 (12)	0.04463 (7)	0.0242 (3)
H2A	0.3615 (11)	0.5722 (11)	0.1135 (7)	0.022 (4)*
H2B	0.3831 (12)	0.5109 (12)	0.0456 (7)	0.024 (3)*
H3A	0.2542 (12)	0.4803 (13)	−0.0592 (7)	0.027 (4)*
H3B	0.1559 (13)	0.5255 (12)	−0.0568 (7)	0.025 (4)*
H4	0.3333	0.6667	−0.1161 (12)	0.022 (6)*
H6	0.0525 (12)	0.4657 (13)	0.1282 (7)	0.025 (4)*
H7	−0.0680 (13)	0.2811 (12)	0.1751 (7)	0.028 (4)*
H8	−0.0503 (13)	0.1156 (14)	0.1410 (7)	0.033 (4)*
H9	0.0922 (12)	0.1449 (13)	0.0574 (7)	0.026 (4)*
H10	0.2155 (12)	0.3292 (12)	0.0115 (7)	0.025 (4)*

Atomic displacement parameters (Ų)

	U^11	U^22	U^33	U^12	U^13	U^23
C1	0.0204 (7)	0.0200 (6)	0.0183 (6)	0.0097 (5)	−0.0010 (5)	−0.0010 (5)
C2	0.0211 (7)	0.0199 (7)	0.0176 (6)	0.0104 (5)	−0.0001 (5)	−0.0001 (5)
C3	0.0251 (7)	0.0240 (7)	0.0193 (7)	0.0120 (6)	−0.0021 (5)	−0.0031 (5)
C4	0.0272 (8)	0.0272 (8)	0.0142 (10)	0.0136 (4)	0.000	0.000
C5	0.0191 (7)	0.0210 (7)	0.0195 (6)	0.0089 (6)	−0.0046 (5)	−0.0019 (5)
C6	0.0228 (7)	0.0208 (7)	0.0246 (7)	0.0099 (6)	−0.0008 (5)	−0.0018 (5)
C7	0.0234 (7)	0.0269 (7)	0.0267 (7)	0.0090 (6)	0.0022 (6)	0.0012 (6)
C8	0.0274 (7)	0.0203 (7)	0.0280 (7)	0.0069 (6)	−0.0032 (6)	0.0034 (6)
C9	0.0296 (8)	0.0213 (7)	0.0284 (7)	0.0138 (6)	−0.0061 (6)	−0.0035 (6)
C10	0.0239 (7)	0.0245 (7)	0.0244 (7)	0.0121 (6)	−0.0011 (6)	−0.0027 (5)

Geometric parameters (Å, º)

C1—C5	1.5236 (17)	C5—C10	1.3989 (17)
C1—C2^i	1.5331 (17)	C6—C7	1.3897 (19)
C1—C2	1.5455 (17)	C6—H6	0.960 (14)
C1—C3	1.5467 (17)	C7—C8	1.3809 (19)
C2—H2A	1.006 (14)	C7—H7	0.979 (15)
C2—H2B	1.034 (14)	C8—C9	1.381 (2)
C3—C4	1.5329 (15)	C8—H8	0.986 (15)
C3—H3A	1.027 (14)	C9—C10	1.3788 (19)
C3—H3B	1.022 (14)	C9—H9	0.957 (16)
C4—H4	1.01 (2)	C10—H10	0.976 (15)
C5—C6	1.3967 (17)
C5—C1—C2^i	112.20 (10)	C3^i—C4—H4	108.82 (9)
C5—C1—C2	108.20 (10)	C3—C4—H4	108.82 (9)
C2^i—C1—C2	108.26 (11)	C3^ii—C4—H4	108.82 (9)
C5—C1—C3	111.49 (10)	C6—C5—C10	117.30 (12)
C2^i—C1—C3	107.91 (10)	C6—C5—C1	122.85 (11)
C2—C1—C3	108.68 (10)	C10—C5—C1	119.73 (11)
C1^ii—C2—C1	112.09 (11)	C7—C6—C5	121.14 (12)
C1^ii—C2—H2A	109.5 (7)	C7—C6—H6	117.9 (8)
C1—C2—H2A	108.5 (8)	C5—C6—H6	121.0 (8)
C1^ii—C2—H2B	108.1 (7)	C8—C7—C6	120.33 (13)
C1—C2—H2B	110.1 (7)	C8—C7—H7	120.9 (8)
H2A—C2—H2B	108.6 (10)	C6—C7—H7	118.7 (8)
C4—C3—C1	109.69 (12)	C7—C8—C9	119.26 (13)
C4—C3—H3A	109.7 (8)	C7—C8—H8	120.0 (9)
C1—C3—H3A	110.4 (8)	C9—C8—H8	120.7 (9)
C4—C3—H3B	110.6 (7)	C10—C9—C8	120.58 (13)
C1—C3—H3B	108.6 (8)	C10—C9—H9	118.8 (8)
H3A—C3—H3B	107.8 (11)	C8—C9—H9	120.6 (8)
C3^i—C4—C3	110.11 (9)	C9—C10—C5	121.35 (12)
C3^i—C4—C3^ii	110.11 (9)	C9—C10—H10	118.4 (8)
C3—C4—C3^ii	110.11 (9)	C5—C10—H10	120.2 (8)
C5—C1—C2—C1^ii	179.82 (8)	C2^i—C1—C5—C10	177.26 (11)
C2^i—C1—C2—C1^ii	−58.36 (16)	C2—C1—C5—C10	−63.37 (14)
C3—C1—C2—C1^ii	58.60 (13)	C3—C1—C5—C10	56.10 (15)
C5—C1—C3—C4	−176.75 (9)	C10—C5—C6—C7	2.05 (18)
C2^i—C1—C3—C4	59.61 (12)	C1—C5—C6—C7	−174.07 (11)
C2—C1—C3—C4	−57.57 (12)	C5—C6—C7—C8	−1.3 (2)
C1—C3—C4—C3^i	−61.40 (13)	C6—C7—C8—C9	−0.3 (2)
C1—C3—C4—C3^ii	60.21 (13)	C7—C8—C9—C10	1.07 (19)
C2^i—C1—C5—C6	−6.71 (16)	C8—C9—C10—C5	−0.27 (19)
C2—C1—C5—C6	112.66 (13)	C6—C5—C10—C9	−1.27 (18)
C3—C1—C5—C6	−127.88 (13)	C1—C5—C10—C9	174.98 (11)

Symmetry codes: (i) −x+y, −x+1, z; (ii) −y+1, x−y+1, z.

(II) 1,3,5,7-Tetraphenyladamantane

Crystal data

C34H32	Dx = 1.235 Mg m^−3
Mr = 440.60	Mo Kα radiation, λ = 0.71073 Å
Tetragonal, P421c	Cell parameters from 4632 reflections
a = 12.8260 (11) Å	θ = 3.2–28.0°
c = 7.2032 (6) Å	µ = 0.07 mm^−1
V = 1184.97 (17) Å^3	T = 213 K
Z = 2	Prism, colorless
F(000) = 472	0.26 × 0.23 × 0.22 mm

Data collection

Stoe IPDS diffractometer	643 reflections with I > 2σ(I)
Radiation source: fine-focus sealed tube	Rint = 0.028
Graphite monochromator	θmax = 28.0°, θmin = 3.2°
ϕ oscillation scans	h = −16→7
4632 measured reflections	k = −16→16
822 independent reflections	l = −8→8

Refinement

Refinement on F^2	Primary atom site location: structure-invariant direct methods
Least-squares matrix: full	Secondary atom site location: difference Fourier map
R[F^2 > 2σ(F^2)] = 0.035	Hydrogen site location: difference Fourier map
wR(F^2) = 0.084	All H-atom parameters refined
S = 0.92	w = 1/[σ^2(Fo^2) + (0.0621P)^2] where P = (Fo^2 + 2Fc^2)/3
822 reflections	(Δ/σ)max < 0.001
110 parameters	Δρmax = 0.24 e Å^−3
0 restraints	Δρmin = −0.14 e Å^−3

Special details

Geometry. All e.s.d.'s (except the e.s.d. in the dihedral angle between two l.s. planes) are estimated using the full covariance matrix. The cell e.s.d.'s are taken into account individually in the estimation of e.s.d.'s in distances, angles and torsion angles; correlations between e.s.d.'s in cell parameters are only used when they are defined by crystal symmetry. An approximate (isotropic) treatment of cell e.s.d.'s is used for estimating e.s.d.'s involving l.s. planes.

Refinement. Refinement of F² against ALL reflections. The weighted R-factor wR and goodness of fit S are based on F², conventional R-factors R are based on F, with F set to zero for negative F². The threshold expression of F² > σ(F²) is used only for calculating R-factors(gt) etc. and is not relevant to the choice of reflections for refinement. R-factors based on F² are statistically about twice as large as those based on F, and R- factors based on ALL data will be even larger.

Fractional atomic coordinates and isotropic or equivalent isotropic displacement parameters (Ų)

	x	y	z	Uiso*/Ueq
C1	0.09921 (11)	−0.00935 (12)	0.1255 (2)	0.0206 (3)
C2	0.0000	0.0000	0.2467 (3)	0.0208 (4)
C3	0.10631 (12)	0.08913 (11)	0.0023 (2)	0.0214 (3)
C4	0.19290 (11)	−0.02061 (13)	0.2568 (2)	0.0243 (4)
C5	0.19726 (14)	−0.10637 (15)	0.3787 (3)	0.0321 (4)
C6	0.27811 (15)	−0.11675 (17)	0.5066 (3)	0.0411 (5)
C7	0.35595 (16)	−0.04211 (19)	0.5169 (3)	0.0462 (5)
C8	0.35344 (15)	0.04244 (18)	0.3983 (3)	0.0423 (5)
C9	0.27237 (12)	0.05320 (15)	0.2690 (3)	0.0317 (4)
H2	−0.0065 (17)	−0.0629 (14)	0.325 (3)	0.031 (5)*
H3A	0.1715 (13)	0.0861 (13)	−0.076 (3)	0.017 (4)*
H3B	0.1113 (14)	0.1522 (15)	0.080 (3)	0.022 (4)*
H5	0.1415 (16)	−0.1612 (15)	0.377 (3)	0.032 (5)*
H6	0.2775 (16)	−0.1757 (17)	0.584 (3)	0.044 (6)*
H7	0.4126 (18)	−0.0507 (17)	0.600 (4)	0.052 (7)*
H8	0.409 (2)	0.0955 (19)	0.404 (4)	0.054 (6)*
H9	0.2703 (16)	0.1148 (15)	0.187 (3)	0.036 (6)*

Atomic displacement parameters (Ų)

	U^11	U^22	U^33	U^12	U^13	U^23
C1	0.0214 (7)	0.0243 (7)	0.0160 (7)	0.0012 (6)	−0.0013 (6)	−0.0004 (6)
C2	0.0235 (10)	0.0221 (10)	0.0168 (10)	0.0006 (9)	0.000	0.000
C3	0.0223 (7)	0.0236 (7)	0.0184 (8)	−0.0017 (5)	0.0000 (7)	−0.0008 (7)
C4	0.0222 (7)	0.0328 (8)	0.0177 (9)	0.0049 (6)	0.0007 (6)	−0.0042 (7)
C5	0.0293 (8)	0.0401 (10)	0.0270 (10)	0.0066 (7)	−0.0015 (7)	0.0017 (8)
C6	0.0387 (10)	0.0568 (12)	0.0278 (10)	0.0168 (9)	−0.0036 (9)	0.0072 (11)
C7	0.0312 (9)	0.0751 (15)	0.0322 (11)	0.0129 (10)	−0.0115 (9)	−0.0069 (11)
C8	0.0265 (9)	0.0609 (13)	0.0397 (12)	−0.0003 (8)	−0.0079 (9)	−0.0108 (11)
C9	0.0256 (8)	0.0408 (10)	0.0287 (10)	0.0008 (7)	−0.0004 (8)	−0.0050 (8)

Geometric parameters (Å, º)

C1—C4	1.536 (2)	C5—C6	1.394 (3)
C1—C3	1.546 (2)	C5—H5	1.00 (2)
C1—C2	1.548 (2)	C6—C7	1.385 (3)
C1—C3^i	1.552 (2)	C6—H6	0.94 (2)
C2—H2	0.987 (19)	C7—C8	1.381 (3)
C3—H3A	1.009 (18)	C7—H7	0.95 (2)
C3—H3B	0.984 (19)	C8—C9	1.403 (3)
C4—C9	1.394 (2)	C8—H8	0.99 (3)
C4—C5	1.409 (3)	C9—H9	0.99 (2)
C4—C1—C3	112.59 (12)	C5—C4—C1	119.24 (13)
C4—C1—C2	107.63 (13)	C6—C5—C4	121.09 (18)
C3—C1—C2	107.98 (11)	C6—C5—H5	118.2 (12)
C4—C1—C3^i	110.79 (12)	C4—C5—H5	120.8 (12)
C3—C1—C3^i	108.62 (11)	C7—C6—C5	120.4 (2)
C2—C1—C3^i	109.14 (11)	C7—C6—H6	122.0 (13)
C1^ii—C2—C1	111.33 (19)	C5—C6—H6	117.6 (13)
C1^ii—C2—H2	108.4 (12)	C8—C7—C6	119.53 (19)
C1—C2—H2	109.1 (13)	C8—C7—H7	119.9 (14)
C1—C3—C1^iii	111.16 (14)	C6—C7—H7	120.5 (14)
C1—C3—H3A	109.7 (10)	C7—C8—C9	120.4 (2)
C1^iii—C3—H3A	109.7 (10)	C7—C8—H8	120.1 (14)
C1—C3—H3B	110.5 (11)	C9—C8—H8	119.6 (15)
C1^iii—C3—H3B	108.6 (10)	C4—C9—C8	121.12 (19)
H3A—C3—H3B	107.1 (14)	C4—C9—H9	119.1 (12)
C9—C4—C5	117.53 (16)	C8—C9—H9	119.8 (12)
C9—C4—C1	123.15 (15)
C4—C1—C2—C1^ii	−178.79 (13)	C2—C1—C4—C5	60.75 (17)
C3—C1—C2—C1^ii	59.42 (10)	C3^i—C1—C4—C5	−58.51 (19)
C3^i—C1—C2—C1^ii	−58.49 (10)	C9—C4—C5—C6	0.0 (3)
C4—C1—C3—C1^iii	−178.78 (14)	C1—C4—C5—C6	−176.72 (17)
C2—C1—C3—C1^iii	−60.10 (15)	C4—C5—C6—C7	0.3 (3)
C3^i—C1—C3—C1^iii	58.14 (12)	C5—C6—C7—C8	−0.5 (3)
C3—C1—C4—C9	3.1 (2)	C6—C7—C8—C9	0.4 (3)
C2—C1—C4—C9	−115.82 (16)	C5—C4—C9—C8	−0.2 (3)
C3^i—C1—C4—C9	124.92 (17)	C1—C4—C9—C8	176.43 (16)
C3—C1—C4—C5	179.64 (15)	C7—C8—C9—C4	0.0 (3)

Symmetry codes: (i) y, −x, −z; (ii) −x, −y, z; (iii) −y, x, −z.