issue contents
September 2003 issue
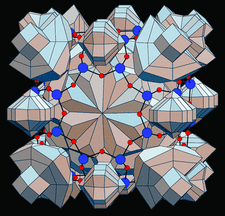
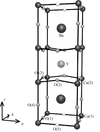
Cover illustration: Polyhedral representation of voids in the sodium-free sublattice of the crystal structure of NaAlSiO4 zeolite. See Blatov & Shevchenko [Acta Cryst. (2003). A59, 34-44].
research papers
Experimental charge density of YBa2Cu3O6.98 from high-energy synchrotron-radiation data and theoretical charge density from LAPW calculations were derived, analysed and compared.
An integer programming formulation and a direct method for the phase problem are developed for centrosymmetric structures. This approach solves the phase problem entirely in reciprocal space.
Open  access
access
 access
accessThe maximum-entropy method (MEM) for the analysis of the electron densities of periodic and aperiodic crystals is critically evaluated. It is shown that the MEM in superspace provides a model-independent reconstruction of the shapes of the modulation functions of incommensurate crystals.
A general equation for fitting interference profiles of three-beam X-ray diffraction is proposed. Phasing procedures for determing the invariant triplet phases in perfect and non-perfect crystals are shown.
Using the lamellar crystal approach, the fundamental set of the differential equations is derived to study interbranch scattering within the new representation called the eikonal representation. It is shown that, in the case of strong bending, an interbranch multiple process may be considered as a resonance one.
Model building based on spherical harmonics–Bessel expansion of the electron density and fast rotation function was developed. A polyalanine chain is built with a high accuracy at resolutions 1.2–2.1 Å using six flexible peptides.
Bonding in α-copper phthalocyanine is studied by quantitative electron diffraction employing the charge-cloud model. A method is proposed to calculate the scattering factors for partially charged ions.
The autocorrelation function of a finite cylindrical particle is expressed as an integral transform of the autocorrelation function of the cylinder right section. The integral transform is inverted to express the second function in terms of the first.
book reviews
Free 

books received
Free 

Free 



 journal menu
journal menu