issue contents
November 2008 issue

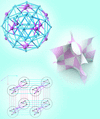
Cover illustration: An octagonal mosaic from the Kasbah de Telouet, High Atlas, Morocco, based on a modified quasilattice. The underlying quasilattice can best be seen in the blue-and-black portions of the pattern where the `standing' lozenges define bars of unit width and the diagonally positioned lozenges define bars with a width equal to ![[square root]](/logos/entities/radic_rmgif.gif) 2. Four orientations of the bar scheme, 45° apart, and phason shifts (alternation of bars in the sequence) are present. Picture taken by Emil Makovicky during the 24th European Crystallographic Meeting 2007.
2. Four orientations of the bar scheme, 45° apart, and phason shifts (alternation of bars in the sequence) are present. Picture taken by Emil Makovicky during the 24th European Crystallographic Meeting 2007.
research papers
short communications
international union of crystallography



 journal menu
journal menu