issue contents
May 2013 issue

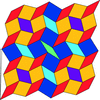
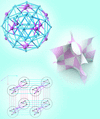
Cover illustration: Symmetric line patterns on the hyperbolic plane can be transformed to weavings of filaments in space via triply periodic minimal surfaces, such as the diamond surface shown. A tight, canonical embedding of this particular weaving is shown, found via a tightening algorithm. Weavings of curvilinear filaments extend the well known crystallographic rod packings, composed of straight rods, widely used in descriptions of crystalline structures [Evans et al. (2013). Acta Cryst. A69, 262-275].
research papers




 journal menu
journal menu