issue contents
May 2023 issue
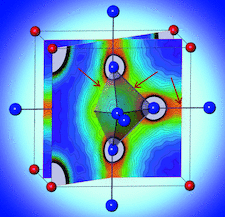
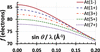
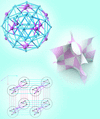
Cover illustration: The electron density (ED) of a chemical system is one of its most fundamental properties, and can in principle be reconstructed by Fourier inversion of the structure factors. However, if this procedure is terminated too early, series truncation artefacts such as spurious local ED maxima and minima can occur, which adversely affect chemical interpretation. In a pilot study in this issue, Bergner et al. [Acta Cryst. (2023), A79, 246–272] reconstruct the static ED for the challenging case of CaB6, exploring different mathematical weighting functions for theoretical structure factors. The image shows the results of a synthesis without employing such weighting functions. Prominent non-nuclear maxima are indicated by red arrows.
foundations
research papers
 access
accesscrystal lattices
 access
access
Boris Gruber's fundamental contributions to the classification of crystal lattices are reviewed.

 journal menu
journal menu