issue contents
September 2023 issue

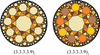
Cover illustration: In this issue, Mazáč [Acta Cryst. (2023), A79, 399–401] presents an efficient algorithm for an exact calculation of patch frequencies for rhombic Penrose tilings. The cover image shows a large patch of the 245 tiles (left) together with its image in the dual space (right). The latter allows one to quickly and exactly compute the frequency of the patch, which can be used in the theory of Schrödinger operators on these structures.
foundations
research papers
 access
access access
access

 access
accesscrystal lattices
 access
access
 journal menu
journal menu