issue contents
Mathematical crystallography special issue (December 2014)
Guest Editor(s): M. Nespolo and G. McColm
This second special issue of Acta Crystallographica Section A on mathematical crystallography contains articles that form a wide but necessarily incomplete selection from the panorama of research activities covered by this field. Some of the articles are based on work that was reported at the 2013 SIAM Conference on Mathematical Aspects of Materials Science in Philadelphia.
This virtual issue collects together a series of articles originally published in the journal between March and July 2014.
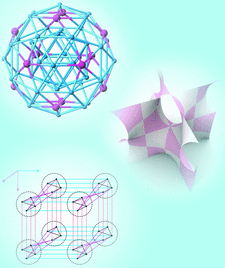
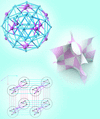
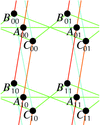
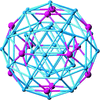
Cover illustration: The mathematical tools used by crystallographers began as abstract models of physical or theoretical structures. As the demand for more powerful tools grows, so grows the demand for sophisticated and fundamental models of crystals and crystalline materials. Clockwise from top left: images from Quiquandon et al. [Acta Cryst. (2014), A70, 229-238], Hyde et al. [Acta Cryst. (2014), A70, 319-337] and Moriera de Oliveira & Eon [Acta Cryst. (2014), A70, 217-228].
The current activities of the IUCr Commission on Mathematical Crystallography are described and the articles in this virtual special issue on mathematical crystallography are introduced.
Considered as an emerging field, how mathematical crystallography grows during the 21st century may depend on how it addresses demand and attracts recruits within the chemical, physical and mathematical communities.
The Brillouin-zone database of the
Bilbao Crystallographic Server (
https://www.cryst.ehu.es) is presented. Recent improvements and modifications of the database are discussed and illustrated by several examples.
The effect of merohedric twinning on the reflection conditions and the symmetry of the diffraction pattern is analysed systematically and criteria to confirm or exclude the presence of twinning are presented.
The recently classified 3-periodic regular apeirohedra and polygonal complexes in space all have well known crystal nets as edge graphs. These nets are determined explicitly.
The central role of bounded automorphisms of finite order in non-crystallographic nets is featured; it is shown that stable nets are crystallographic nets.
Materials invariant under infinite subsets of line groups are shown to have physical property tensors of the same form.
The basic tools commonly used to describe the atomic structures of quasicrystals are presented, with a specific focus on the icosahedral phases.
The discrete groups of isometries of the two-dimensional sphere, flat (euclidean) plane and the hyperbolic plane are described and unified using orbifolds. A simple classification schema for orbifolds is proposed that allows systematic exploration of the vast wealth of hyperbolic examples. The article also tabulates space groups that form by decorating simpler triply periodic minimal surfaces with so-called crystallographic hyperbolic orbifolds.




 journal menu
journal menu