issue contents
July 2020 issue

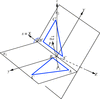
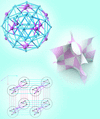
Cover illustration: Finding the unique rotation that best aligns two sets of geometric data is a fundamental problem in many domains, from structural biochemistry and aerospace problems to machine vision and digital heritage applications. Quaternion methods are particularly useful for solving this problem given 3D or 4D data, as shown by A. J. Hanson [Acta Cryst. (2020). A76, 432-457] in this issue. Known methods for aligning 3D data sets such as pairs of matched protein structures are reviewed, and then extended to other domains such as orientation frames: this visualization illustrates the challenging properties of the ambiguous quaternion basins of attraction that appear for unconstrained orientation-frame data.
advances
lead articles
 access
accessfoundations
research papers


 access
accessbook reviews





 journal menu
journal menu