issue contents
January 2022 issue

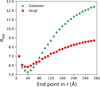
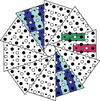
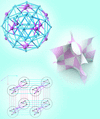
Cover illustration: Understanding the properties of primitive substitution tilings is of increasing relevance not only to various fields of mathematics, but also to the study of crystals and quasicrystals for which tilings are used as structure models. One property is the frequency module of the hull of a primitive substitution tiling, which contains the frequency of each patch of the tiling. Because the frequency module of the hull of a primitive substitution tiling cannot always be derived from its corresponding substitution, a technique used by Say-awen et al. [Acta Cryst. (2022). A78, 36–55] is to introduce a new substitution, which arises from a partition of the tiling satisfying certain conditions. The cover image shows a portion of a partition of a particular primitive substitution tiling.
foundations
research papers
 access
accessshort communications
book reviews

obituaries

international union of crystallography



 journal menu
journal menu