issue contents
March 2022 issue

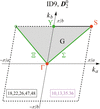
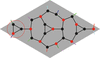
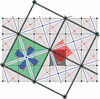
Cover illustration: The two commonly used systems of magnetic space-group symbols are those of Belov–Neronova–Smirnova (BNS) and Opechowski–Guccione (OG). Both present challenges of interpretation to novice and expert users alike, which can inhibit understanding and lead to errors in published magnetic structures. To address these challenges going forward, Campbell et al. [Acta Cryst. (2022). A78, 99–106] introduce a new unified (UNI) magnetic space-group symbol, which combines a modified BNS symbol with essential information from the OG symbol. The cover image illustrates a pattern of magnetic moments surrounding the origin of the magnetic space group Pm′-3′, for which the magnetic point group is m′-3′. Operators shown in yellow are time reversed, whereas those shown in blue are not. Magnetic moments are presented as arrows; moments of opposite colors are related by an improper operation. (Image taken from Marc De Graef's web site https://mpg.web.cmu.edu/ with permission.)
advances
research papers
foundations
research papers
 access
access

 journal menu
journal menu