issue contents
March 2025 issue
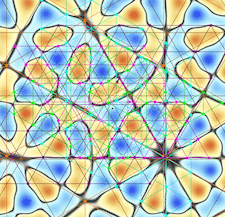
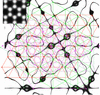
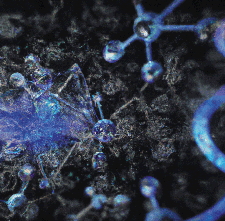
Cover illustration: In this issue Quiquandon & Gratias [Acta Cryst. (2025), A81, 94–106] provide a novel crystallographic framework for twisted bilayer systems. In the image, the black curves separate the positive (red tones) and negative (blue tones) regions of the difference between the electron densities of two identical graphene monolayers twisted by 13.359° and translated by (0.15,0.35) in graphene coordinates. The points of the six phi-lattices (orange phi=0, purple phi=π/3, green phi=2π/3, magenta phi=π, cyan phi=4π/3, brown phi=5π/3) made of the infinitely many equivalent local twist rotation centers are systematically all on these curves and do not depend on the atomic structure of the layer. These invariant lattices are generic regardless of the possible existence of a coincidence lattice that arises only for an enumerable set of rotations. They exist for any crystalline system, vary continuously with the twist angles and characterize the actual crystallographic properties of the general homophase twisted bilayers.
obituaries


scientific commentaries

advances
research papers
 access
accessfoundations
research papers
 access
access access
access access
access access
access
 journal menu
journal menu