issue contents
May 2020 issue
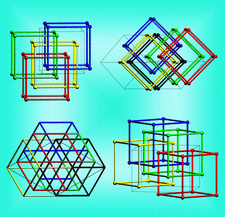
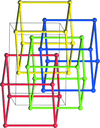
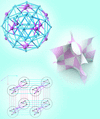
Cover illustration: In their Lead Article, Power et al. [Acta Cryst. (2020). A76, 275-301] develop new mathematical tools to classify and enumerate isotopy types for 3-periodic nets. Isotopy types are aimed at distinguishing different aspects of (self-)catenation observed in crystal structures. As a first step, they classify 3-periodic bouquet nets and n-fold pcu nets up to periodic isotopy. The image illustrates some of the enumerated four- and fivefold pcu nets which could represent challenging targets for synthetic chemists.
scientific commentaries

advances
lead articles
 access
accessresearch papers
foundations
research papers
 access
access access
access access
access access
access



 journal menu
journal menu